Graph and Segment Trees
tags:icpc
algorithm
segment-tree
graph
under-construction
Outline
- What is this post about?
- Example problems - Shortest path
- Example problems - Flow
- Example problems - DP on DAG
- More problems
What is this post about?
In this post, you’ll see how to use segment trees to optimize graph construction. We’ll go through several examples to demonstrate this technique.
Example problems - Shortest path
CF787D - Legacy
Problem description
You’re given an empty graph $G$ with $N$ nodes in it. Now, you need to add edges to the graph by the following three operations:
- $1\space u\space v\space w$ : Add a edge from $u$ to $v$ weighted $w$
- $2\space u\space l\space r\space w$ : Add edges from $u$ to $v=l, l+1, \dots, r$ with weight $w$
- $3\space v\space l\space r\space w$ : Add edges from $u=l, l+1 \dots, r$ to $v$ with weight $w$
There’re $Q$ operations in total. Please calculate the shortest path for all nodes starting from node $s$.
$1\le N, Q\le 10^5, 1\le s \le n, 1\le l, r, u, v\le N, l\le r, 1\le w\le 10^9$
Problem analysis
Obviously, we can’t build the graph directly. Observe that every time we add edges, either the start or the end of edges are continuous. Therefore, we can build two segment trees like the following:
picture
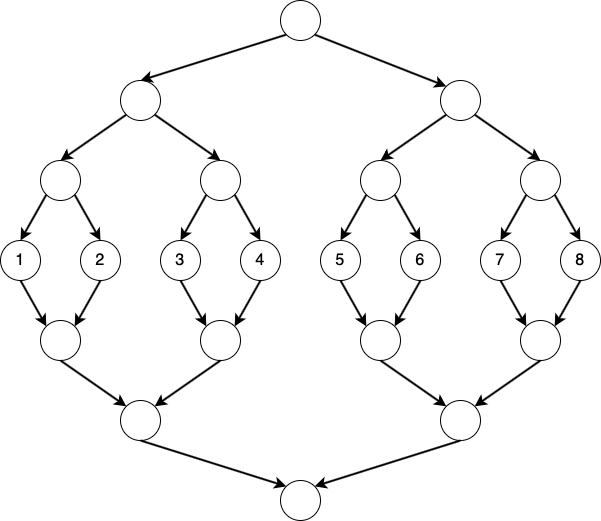
Arrows are edges with weight $0$. The leaf node are the original nodes in graph $G$.
For type two operations, we add $O(\log N)$ edges from $u$ to the nodes that correspond to $[l, r]$ with weight $w$.
For example, if we want to add edge from $1$ to $[2, 6]$, then:
picture
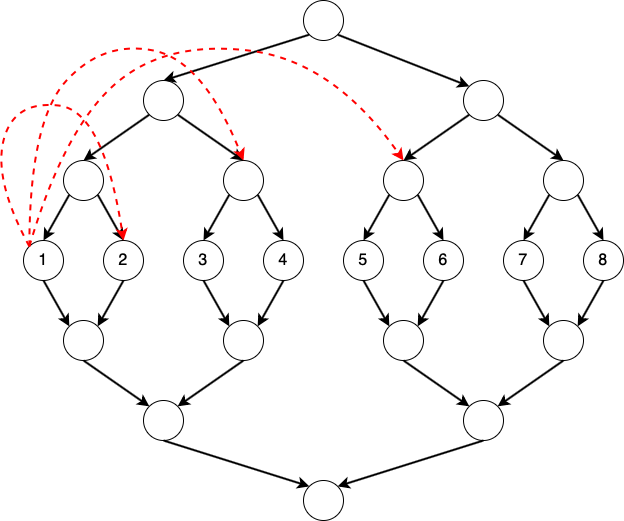
For type three operations, we add $O(\log N)$ edges from nodes that correspond to $[l, r]$ to $v$ with weight $w$.
For example, if we want to add edge from $[4, 8]$ to $2$, then:
picture
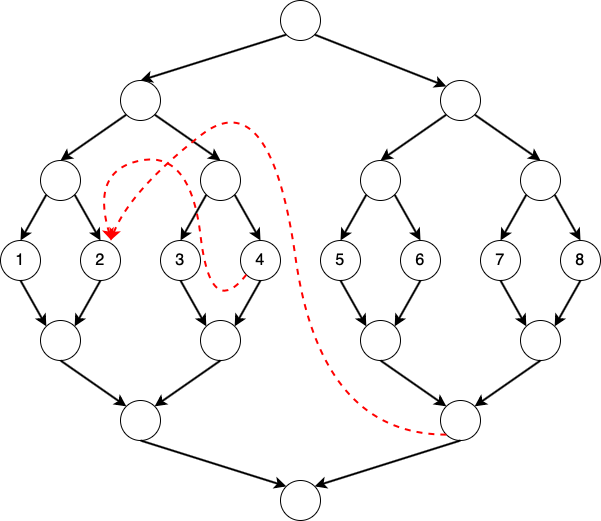
Problem solution
The number of nodes is $O(3N)$, and the number of edges is $O(2N + Q\log N)$, which are both acceptable. The final time complexity is $O(E\log V)=O((2N+Q\log N)\log 3N)$. Details in code.
code
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N = (int)1e5 + 5;
const ll inf = (ll)1e18;
vector<pair<int, int> > G[N * 3];
int n, q, s, n2, ls[N * 3], rs[N * 3];
ll d[N * 3];
pair<int, int> build(int l, int r) {
if(l + 1 == r) return {l, l};
int mid = (l + r) >> 1, o1 = n2++, o2 = n2++;
auto [l1, l2] = build(l, mid);
auto [r1, r2] = build(mid, r);
G[o1].push_back({l1, 0}); G[o1].push_back({r1, 0});
ls[o1] = l1; rs[o1] = r1;
G[l2].push_back({o2, 0}); G[r2].push_back({o2, 0});
ls[o2] = l2; rs[o2] = r2;
return {o1, o2};
}
void insert1(int l, int r, int ql, int qr, int u, int w, int o) {
if(ql <= l && r <= qr) {
G[u].push_back({o, w});
return;
}
int mid = (l + r) >> 1;
if(qr <= mid) insert1(l, mid, ql, qr, u, w, ls[o]);
else if(mid <= ql) insert1(mid, r, ql, qr, u, w, rs[o]);
else {
insert1(l, mid, ql, mid, u, w, ls[o]);
insert1(mid, r, mid, qr, u, w, rs[o]);
}
}
void insert2(int l, int r, int ql, int qr, int v, int w, int o) {
if(ql <= l && r <= qr) {
G[o].push_back({v, w});
return;
}
int mid = (l + r) >> 1;
if(qr <= mid) insert2(l, mid, ql, qr, v, w, ls[o]);
else if(mid <= ql) insert2(mid, r, ql, qr, v, w, rs[o]);
else {
insert2(l, mid, ql, mid, v, w, ls[o]);
insert2(mid, r, mid, qr, v, w, rs[o]);
}
}
void init() {
cin >> n >> q >> s;
n2 = n + 1;
auto [root1, root2] = build(1, n + 1);
while(q--) {
int op = 1; cin >> op;
if(op == 1) {
int u, v, w; cin >> u >> v >> w;
G[u].push_back({v, w});
}
else if(op == 2) {
int u, l, r, w; cin >> u >> l >> r >> w;
insert1(1, n + 1, l, r + 1, u, w, root1);
}
else {
int v, l, r, w; cin >> v >> l >> r >> w;
insert2(1, n + 1, l, r + 1, v, w, root2);
}
}
}
void solve() {
fill(d, d + n2, -1);
d[s] = 0;
priority_queue<pair<ll, int>, vector<pair<ll, int> >, greater<pair<ll, int> > > pq;
pq.push({d[s], s});
while(!pq.empty()) {
auto [_, u] = pq.top(); pq.pop();
for(auto [v, w] : G[u]) {
if(d[u] + w < d[v] || d[v] == -1) {
d[v] = d[u] + w;
pq.push({d[v], v});
}
}
}
for(int i = 1 ; i <= n ; ++i) cout << d[i] << ' ';
cout << '\n';
}
int main() {
ios_base::sync_with_stdio(0), cin.tie(0);
init();
solve();
}
HDU5669 - Road
Problem description
Given a empty graph $G$ with $N$ nodes, you need to add edges to the graph $M$ times. The format of every addition is $(a, b, c, d, w)$, meaning that there exist an undirected edge with weight $w$ between every pair $(x, y)$ where $x\in [a, b], y\in [c, d]$.
Now, you have $K$ times to fly over an edge $(u, v, w)$, which means that you don’t need to pay the cost $w$. Please calculate the minimum cost from node $1$ to node $N$.
$1\le N\le 5\times 10^4, 1\le M\le 10^4, 0\le K\le 10, 1\le w\le 10^3$
Problem analysis
The $K$ chance to fly can be easily handled by adding a dimension to the state.
Similar to the previous problem, we first build two segment trees with the leaves as original nodes.
To handle the addition, we just create $O(\log^2 N)$ edges between nodes that correspond to $[a, b]$ and nodes that correspond to $[c, d]$ with weight $w$.
For example, if we want to add edge between $[3, 5]$ and $[6, 8]$, then:
picture
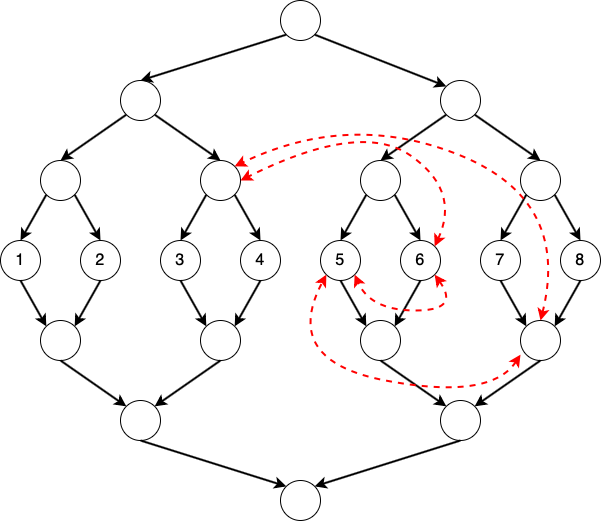
Note that number of edges can be optimized to $O(\log N)$ if we create an extra node every addition.
Problem solution
As we have $O(3NK)$ states (not nodes) and $O(2N + M\log^2 N)$ edges, the time complexity is $O((2N + M\log^2 N)\log 3NK)$.
code
#include <iostream>
#include <queue>
#include <vector>
#include <functional>
#define F first
#define S second
using namespace std;
typedef long long ll;
typedef pair<int, int> pii;
const int N = (int)5e4 + 5;
const int K = 10 + 1;
const int inf = (int)1e9;
int n, m, k, n2, root1, root2, d[K][N * 3], lson[N * 3], rson[N * 3];
vector<pair<int, int> > G[N * 3];
pii build(int l, int r) {
if(l + 1 == r) return {l, l};
int mid = (l + r) >> 1, o1 = n2++, o2 = n2++;
pii ls = build(l, mid); int l1 = ls.F, l2 = ls.S;
pii rs = build(mid, r); int r1 = rs.F, r2 = rs.S;
lson[o1] = l1; rson[o1] = r1;
lson[o2] = l2; rson[o2] = r2;
G[o1].push_back({l1, 0}); G[o1].push_back({r1, 0});
G[l2].push_back({o2, 0}); G[r2].push_back({o2, 0});
return {o1, o2};
}
void insert2(int l, int r, int ql, int qr, int v, int w, int o=root2) {
if(ql <= l && r <= qr) {
G[o].push_back({v, w});
return;
}
int mid = (l + r) >> 1;
if(qr <= mid) insert2(l, mid, ql, qr, v, w, lson[o]);
else if(mid <= ql) insert2(mid, r, ql, qr, v, w, rson[o]);
else {
insert2(l, mid, ql, mid, v, w, lson[o]);
insert2(mid, r, mid, qr, v, w, rson[o]);
}
}
void insert1(int l, int r, int ql, int qr, int ql2, int qr2, int w, int o=root1) {
if(ql <= l && r <= qr) {
insert2(1, n + 1, ql2, qr2, o, w);
return;
}
int mid = (l + r) >> 1;
if(qr <= mid) insert1(l, mid, ql, qr, ql2, qr2, w, lson[o]);
else if(mid <= ql) insert1(mid, r, ql, qr, ql2, qr2, w, rson[o]);
else {
insert1(l, mid, ql, mid, ql2, qr2, w, lson[o]);
insert1(mid, r, mid, qr, ql2, qr2, w, rson[o]);
}
}
void init() {
cin >> n >> m >> k;
for(int i = 0 ; i <= n * 3 ; ++i) G[i].clear();
n2 = n + 1;
pii rr = build(1, n + 1);
root1 = rr.F, root2 = rr.S;
while(m--) {
int a, b, c, D, w; cin >> a >> b >> c >> D >> w;
insert1(1, n + 1, a, b + 1, c, D + 1, w);
insert1(1, n + 1, c, D + 1, a, b + 1, w);
}
}
void solve() {
for(int i = 0 ; i <= k ; ++i) fill(d[i], d[i] + n2, inf);
d[0][1] = 0;
priority_queue<pair<int, pii>, vector<pair<int, pii> >, greater<pair<int, pii> > > pq;
pq.push({d[0][1], {0, 1}});
while(!pq.empty()) {
auto p = pq.top(); pq.pop();
int uk = p.S.F, u = p.S.S;
for(auto pp : G[u]) {
int v = pp.F, w = pp.S;
if(d[uk][u] + w < d[uk][v]) {
d[uk][v] = d[uk][u] + w;
pq.push({d[uk][v], {uk, v}});
}
if(uk < k && d[uk + 1][v] > d[uk][u]) {
d[uk + 1][v] = d[uk][u];
pq.push({d[uk + 1][v], {uk + 1, v}});
}
}
}
int ans = inf;
for(int i = 0 ; i <= k ; ++i) ans = min(ans, d[i][n]);
if(ans == inf) cout << "CreationAugust is a sb!\n";
else cout << ans << '\n';
}
int main() {
ios_base::sync_with_stdio(0), cin.tie(0);
int t; cin >> t;
while(t--) {
init();
solve();
}
}
Example problems - Flow
CF793G - Oleg and chess
Problem description
Given a board with size $N\times N$, you want to put a bunch of rooks on it. However, there are $Q$ rectangles $(x_1, y_1, x_2, y_2)$ specifying that you cannot put anything in the rectangle area with lower-left cell $(x_1, y_1)$, upper-right cell $(x_2, y_2)$ on the board. Also, if you’ve put a rook on $(x, y)$ already, then you cannot put any rooks on $(x, i), (i, y), i\in [1, n]$.
Please output the maximum number of rooks that can be put on the board not violating the rules specified.
$1\le N\le 10^4, 0\le Q\le 10^4, 1\le x_1 \le x_2\le N, 1\le y_1 \le y_2 \le N$
Problem analysis
Observe that if we create $2N$ nodes, and for every valid position $(i, j)$, we connect an edge between $i$ and $j$. Then the original problem is exactly maximum matching on the graph, which can be solved by maximum flow.
Thus, we create a segment tree to optimize our graph construction, and run dinic algorithm on it.
Problem solution
Details are given in code. I used persistent segment tree to help graph construction. For more details please refer to the code.
code
#include <bits/stdc++.h>
#define PB push_back
using namespace std;
typedef long long ll;
const int N = 20000 + 5;
const int M = (int)3e6 + 10;
const int inf = (int)1e9;
struct Dinic{
static const int MXN = M;
struct Edge{ int v,f,re; };
int n,s,t,level[MXN];
vector<Edge> E[MXN];
void init(int _n, int _s, int _t){
n = _n; s = _s; t = _t;
//for (int i=0; i<n; i++) E[i].clear();
}
void add_edge(int u, int v, int f){
E[u].PB({v,f,(int)E[v].size()});
E[v].PB({u,0,(int)E[u].size()-1});
}
bool BFS(){
for (int i=0; i<n; i++) level[i] = -1;
queue<int> que;
que.push(s);
level[s] = 0;
while (!que.empty()){
int u = que.front(); que.pop();
for (auto &it : E[u]){
if (it.f > 0 && level[it.v] == -1){
level[it.v] = level[u]+1;
que.push(it.v);
}
}
}
return level[t] != -1;
}
int DFS(int u, int nf){
if (u == t) return nf;
int res = 0;
for (auto &it : E[u]){
if (it.f > 0 && level[it.v] == level[u]+1){
int tf = DFS(it.v, min(nf,it.f));
res += tf; nf -= tf; it.f -= tf;
E[it.v][it.re].f += tf;
if (nf == 0) return res;
}
}
if (!res) level[u] = -1;
return res;
}
int flow(int res=0){
while ( BFS() )
res += DFS(s,2147483647);
return res;
}
} flow;
struct Node {
int l, r, v;
};
int n, m, s, t, tot;
vector<Node> seg[N];
namespace segtree {
int id[N * 4], tag[N * 4];
inline void pull(int o) {
id[o] = ++tot;
if(!tag[o * 2 + 1]) flow.add_edge(id[o], id[o * 2 + 1], inf);
if(!tag[o * 2 + 2]) flow.add_edge(id[o], id[o * 2 + 2], inf);
}
void build(int l, int r, int o=0) {
if(l + 1 == r) return void(id[o] = n + l);
int mid = (l + r) >> 1, lson = o * 2 + 1, rson = o * 2 + 2;
build(l, mid, lson);
build(mid, r, rson);
pull(o);
}
void modify(int l, int r, int ql, int qr, int v, int o=0) {
if(ql <= l && r <= qr) return void(tag[o] += v);
int mid = (l + r) >> 1, lson = o * 2 + 1, rson = o * 2 + 2;
if(ql < mid) modify(l, mid, ql, qr, v, lson);
if(qr > mid) modify(mid, r, ql, qr, v, rson);
pull(o);
}
}
void init() {
cin >> n >> m;
tot = 2 * n + 1, s = 0, t = 2 * n + 1;
for(int i = 1 ; i <= m ; ++i) {
int x1, y1, x2, y2; cin >> x1 >> y1 >> x2 >> y2;
seg[y1].push_back({x1, x2 + 1, 1});
seg[y2 + 1].push_back({x1, x2 + 1, -1});
}
}
void solve() {
for(int i = 1 ; i <= n ; ++i) {
flow.add_edge(s, i, 1);
flow.add_edge(i + n, t, 1);
}
segtree::build(1, n + 1);
for(int i = 1 ; i <= n ; ++i) {
for(auto [l, r, v] : seg[i]) segtree::modify(1, n + 1, l, r, v);
if(!segtree::tag[0]) flow.add_edge(i, segtree::id[0], inf);
}
flow.init(tot + 1, s, t);
cout << flow.flow() << '\n';
}
int main() {
ios_base::sync_with_stdio(0), cin.tie(0);
init();
solve();
}
Example problems - DP on DAG
POI XXII PUS - Desert
Problem description
You’re given an array $A$ with length $N$ but you only know $S$ elements in it. Moreover, you’re given $M$ description of $A$. Every description is in the following format:
$$ l\space r\space k\space x_1\space x_2\space \dots x_k : \min_{i\in \left\{ x_1, x_2, \dots, x_k \right\}} A_i \ge \max_{i\in [l, r], i\not\in \left\{ x_1, x_2, \dots, x_k \right\}} A_i $$
If exist some $A$ with $1\le A_i\le 10^9, i\in [1, N]$ satisfying the given description and inital elements, output $TAK$ and any possible $A$. Otherwise, output $NIE$.
$1\le S\le N\le 10^5, 1\le M\le 2\times 10^5, \sum k \le 2\times 10^5$
Problem analysis
Problem solution
code
#include <bits/stdc++.h>
#define F first
#define S second
using namespace std;
typedef long long ll;
typedef pair<int, int> pii;
const int N = (int)1e5 + 5;
int n, s, m, n2, d[N * 5], lson[N * 5], rson[N * 5], val[N];
int root1, root2, in[N * 5];
vector<pii> G[N * 5];
pii build(int l, int r) {
if(l + 1 == r) return {l, l};
int mid = (l + r) >> 1, o1 = n2++, o2 = n2++;
auto [l1, l2] = build(l, mid);
auto [r1, r2] = build(mid, r);
lson[o1] = l1, rson[o1] = r1; lson[o2] = l2, rson[o2] = r2;
G[o1].push_back({l1, 0}); G[o1].push_back({r1, 0});
G[l2].push_back({o2, 0}); G[r2].push_back({o2, 0});
return {o1, o2};
}
void insert2(int l, int r, int ql, int qr, int v, int w, int o=root2) {
if(ql <= l && r <= qr) {
G[o].push_back({v, w});
return;
}
int mid = (l + r) >> 1;
if(qr <= mid) insert2(l, mid, ql, qr, v, w, lson[o]);
else if(mid <= ql) insert2(mid, r, ql, qr, v, w, rson[o]);
else {
insert2(l, mid, ql, mid, v, w, lson[o]);
insert2(mid, r, mid, qr, v, w, rson[o]);
}
}
void init() {
cin >> n >> s >> m;
while(s--) {
int p, x; cin >> p >> x; val[p] = d[p] = x;
}
n2 = n + 1;
auto _ = build(1, n + 1); root1 = _.F, root2 = _.S;
while(m--) {
int l, r, k; cin >> l >> r >> k;
for(int i = 0 ; i < k ; ++i) {
int x; cin >> x;
if(l < x) insert2(1, n + 1, l, x, n2, 0);
G[n2].push_back({x, 1});
l = x + 1;
}
if(l <= r) insert2(1, n + 1, l, r + 1, n2, 0);
n2++;
}
}
void solve() {
for(int i = 1 ; i < n2 ; ++i) {
for(auto [v, w] : G[i]) in[v]++;
}
queue<int> q;
for(int i = 1 ; i < n2 ; ++i) {
if(!d[i]) d[i] = 1, val[i] = (int)1e9;
if(!in[i]) q.push(i);
}
while(!q.empty()) {
int u = q.front(); q.pop();
for(auto [v, w] : G[u]) {
d[v] = max(d[v], d[u] + w);
if(val[v] != (int)1e9 && val[v] < d[v]) { cout << "NIE\n"; return; }
if(!--in[v]) q.push(v);
}
}
for(int i = 1 ; i <= n ; ++i) {
if(in[i] || d[i] > (int)1e9) { cout << "NIE\n"; return; }
}
cout << "TAK\n";
for(int i = 1 ; i <= n ; ++i) {
cout << d[i] << " \n"[i == n];
}
}
int main() {
ios_base::sync_with_stdio(0), cin.tie(0);
init();
solve();
}
CF1197E - Culture Code
Problem description
You’re given $N$ boxes. Every box has two attributes, $out$ and $in$ ($in < out$), specifying the total space of the box and the inner space of the box. A box $i$ can be put into a box $j$ iff $out_i \le in_j$.
Now, given a sequence of box $a_1, a_2, \dots, a_k$ satisfying $out_{a_1} \le in_{a_2}$ (such sequence is called valid sequence), the extra space of them is defined by $in_{a_1} + \sum_{i=2}^{k} in_{a_i} - out_{a_{i-1}}$.
A set of boxes is valid if:
- Exist an arrangement of element in the box such that it’s a valid sequence and minimize extra space
- Adding any other box into this set will make it invalid
Please output the number of valid set module $10^9+7$.
$1\le N\le 2\times 10^5, 1\le in\le out\le 10^9$
Problem analysis
Problem solution
code
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N = (int)2e5 + 5;
const int M = (int)1e9 + 7;
struct Doll {
int out, in;
};
int n, n2, root, s, t, lson[N * 3], rson[N * 3], in_pre[N], in[N * 3];
ll d[N * 3], cnt[N * 3];
vector<Doll> doll;
vector<pair<int, int> > G[N * 3];
int build(int l, int r) {
int mid = (l + r) >> 1, o = n2++;
if(l + 1 == r) {
G[o].push_back({l, -doll[l].out});
}
else {
lson[o] = build(l, mid); G[o].push_back({lson[o], 0});
rson[o] = build(mid, r); G[o].push_back({rson[o], 0});
}
return o;
}
void insert(int l, int r, int ql, int qr, int u, int w, int o=root) {
if(ql <= l && r <= qr) {
G[u].push_back({o, w});
return;
}
int mid = (l + r) >> 1;
if(qr <= mid) insert(l, mid, ql, qr, u, w, lson[o]);
else if(mid <= ql) insert(mid, r, ql, qr, u, w, rson[o]);
else {
insert(l, mid, ql, mid, u, w, lson[o]);
insert(mid, r, mid, qr, u, w, rson[o]);
}
}
void init() {
cin >> n;
for(int i = 0 ; i < n ; ++i) {
int a, b; cin >> a >> b; doll.push_back({a, b});
}
sort(doll.begin(), doll.end(), [&](auto a, auto b) { return a.out < b.out; });
n2 = n; root = build(0, n);
s = n2++, t = n2++;
for(int i = 0 ; i < n ; ++i) {
Doll target = {doll[i].in, (int)1e9};
int j = upper_bound(doll.begin(), doll.end(), target, [&](auto a, auto b) { return a.out < b.out; }) - doll.begin();
if(j > 0) {
insert(0, n, 0, j, i, doll[i].in);
in_pre[0]++; in_pre[j]--;
}
else G[i].push_back({t, doll[i].in});
}
int in_deg = 0;
for(int i = 0 ; i < n ; ++i) {
in_deg += in_pre[i];
if(in_deg == 0) G[s].push_back({i, 0});
}
}
void solve() {
for(int i = 0 ; i < n2 ; ++i) {
for(auto [v, w] : G[i]) in[v]++;
}
vector<int> topo;
queue<int> q;
for(int i = 0 ; i < n2 ; ++i) if(!in[i]) q.push(i);
while(!q.empty()) {
int u = q.front(); q.pop(); topo.push_back(u);
for(auto [v, w] : G[u]) {
if(!--in[v]) q.push(v);
}
}
fill(d, d + n2, (ll)1e18); d[s] = 0;
for(auto u : topo) {
for(auto [v, w] : G[u]) d[v] = min(d[v], d[u] + w);
}
cnt[s] = 1;
for(auto u : topo) {
for(auto [v, w] : G[u]) if(d[v] == d[u] + w) cnt[v] = (cnt[u] + cnt[v]) % M;
}
cout << cnt[t] << '\n';
}
int main() {
ios_base::sync_with_stdio(0), cin.tie(0);
init();
solve();
}
BZOJ5017 - Bomb
Problem description
There’s $N$ bombs on a number line. Every bomb is placed at $x_i$, with explosion radius $r_i$. When a bomb explodes, all bombs $j$ with $x_i-r_i\le x_j\le x_i+r_i$ will explodes, too.
Now, let $c_i$ be the number of bombs that will explode if we manually activate the $i^{th}$ bomb. Please calculate $\left(\sum_{i=1}^{N}ic_i\right)\mod 10^9+7$.
$1\le N\le 5\times 10^5, -10^{18} \le x_i \le 10^{18}, 0\le r_i\le 2\times 10^{18}$
Problem analysis
Problem solution
code
#pragma GCC optimize ("O3,no-stack-protector,unroll-loops")
#include <algorithm>
#include <iostream>
#include <vector>
#define F first
#define S second
using namespace std;
typedef long long ll;
const int N = (int)5e5 + 5;
const int M = (int)1e9 + 7;
int n, n2, root;
vector<int> G[N * 2], G2[N * 2], stk;
vector<ll> v;
vector<pair<ll, ll> > bomb;
int pre[N * 2], low[N * 2], scc[N * 2], vis[N * 2], lef[N * 2], rig[N * 2], clk, cnt;
namespace graph {
struct Node {
int l, r, ls, rs;
} a[N * 2];
int build(int l, int r) {
if(l + 1 == r) {
a[l] = {l, r, -1, -1};
return l;
}
int mid = (l + r) >> 1, o = n2++, lson = build(l, mid), rson = build(mid, r);
G[o].push_back(lson);
G[o].push_back(rson);
a[o] = {l, r, lson, rson};
return o;
}
void insert(int l, int r, int ql, int qr, int u, int o=root) {
if(ql <= l && r <= qr) {
if(u != o) G[u].push_back(o);
return;
}
int mid = (l + r) >> 1, lson = a[o].ls, rson = a[o].rs;
if(qr <= mid) insert(l, mid, ql, qr, u, lson);
else if(mid <= ql) insert(mid, r, ql, qr, u, rson);
else {
insert(l, mid, ql, mid, u, lson);
insert(mid, r, mid, qr, u, rson);
}
}
void tarjan(int u) {
pre[u] = low[u] = ++clk; vis[u] = 1;
stk.push_back(u);
for(int i = 0 ; i < (int)G[u].size() ; ++i) {
int v = G[u][i];
if(!pre[v]) {
tarjan(v);
low[u] = min(low[u], low[v]);
}
else if(vis[v]) {
low[u] = min(low[u], pre[v]);
}
}
if(low[u] == pre[u]) {
lef[cnt] = n, rig[cnt] = 0;
while(1) {
int x = stk.back(); stk.pop_back();
lef[cnt] = min(lef[cnt], a[x].l);
rig[cnt] = max(rig[cnt], a[x].r);
scc[x] = cnt;
if(x == u) break;
}
++cnt;
}
}
void buildG2() {
for(int u = 0 ; u < n2 ; ++u) {
for(int i = 0 ; i < (int)G[u].size() ; ++i) {
int v = G[u][i];
if(scc[u] != scc[v]) G2[scc[u]].push_back(scc[v]);
}
}
for(int u = 0 ; u < cnt ; ++u) {
sort(G2[u].begin(), G2[u].end());
G2[u].resize(unique(G2[u].begin(), G2[u].end()) - G2[u].begin());
}
}
void dfs(int u) {
vis[u] = 1;
for(int i = 0 ; i < (int)G2[u].size() ; ++i) {
int v = G2[u][i];
if(!vis[v]) dfs(v);
lef[u] = min(lef[u], lef[v]);
rig[u] = max(rig[u], rig[v]);
}
}
int query(int u) {
return rig[scc[u]] - lef[scc[u]];
}
}
void init() {
cin >> n;
for(int i = 0 ; i < n ; ++i) {
ll x, r; cin >> x >> r;
bomb.push_back({x, r});
v.push_back(x);
}
n2 = n;
root = graph::build(0, n);
for(int i = 0 ; i < n ; ++i) {
int l = lower_bound(v.begin(), v.end(), bomb[i].F - bomb[i].S) - v.begin();
int r = upper_bound(v.begin(), v.end(), bomb[i].F + bomb[i].S) - v.begin();
graph::insert(0, n, l, r, i);
}
}
void solve() {
graph::tarjan(root);
graph::buildG2();
fill(vis, vis + cnt, 0);
for(int i = 0 ; i < cnt ; ++i) if(!vis[i]) graph::dfs(i);
int ans = 0;
for(int i = 0 ; i < n ; ++i) ans = (ans + (ll)graph::query(i) * (i + 1)) % M;
cout << ans << '\n';
}
int main() {
ios_base::sync_with_stdio(0), cin.tie(0);
init();
solve();
}