Sweep Line and Segment Trees
tags:icpc
algorithm
segment-tree
geometry
sweep-line
Outline
What is this post about?
Demonstrate some well-known usage of sweep line with segment tree. The most classic type of problem that this technique can solve is rectangle union area/perimeter.
Example problems
TIOJ1224 - Rectangle union area (Chinese)
Problem description
Given $N$ rectangles described by $L_i, R_i, D_i, U_i$ , representing that the $i^{th}$ bottom-left corner of the rectangle is $(L_i, D_i)$ , and the top-right corner of the rectangle is $(R_i, U_i)$ , please calculate the union area of those $N$ rectangles.
$1\le N\le 10^5, 0\le L_i < R_i \le 10^6, 0\le D_i < U_i \le 10^6$
Problem analysis
A classic type of problem that sweep line + segment tree can solve. Let see the algorithm by example.
example
Suppose in the beginning, we’re given these rectangles:
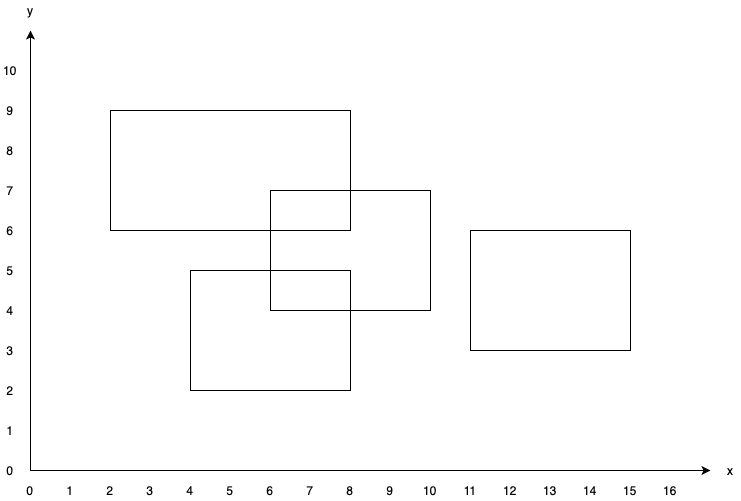
Now, we sweep a line starting from $y=0$.
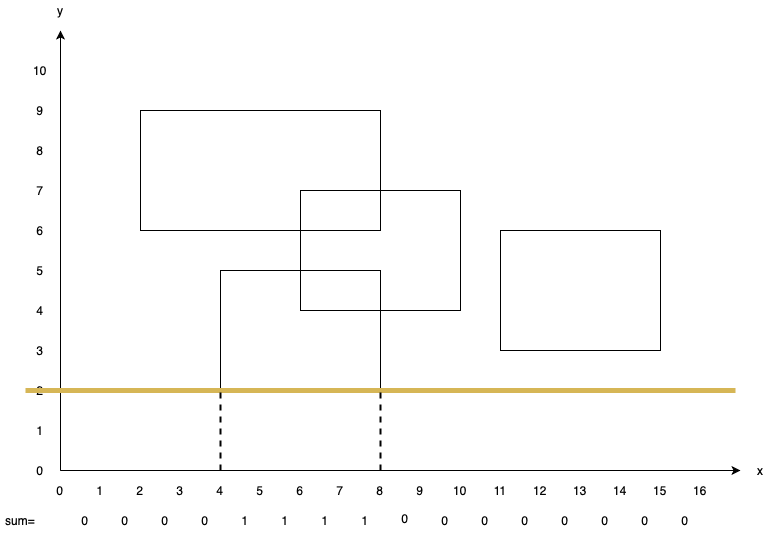
We’ll stop at $y=2$, as we met a bottom edge of some rectangle. We add $1$ to $sum[4, 5, 6, 7]$. Then, we continue sweeping.
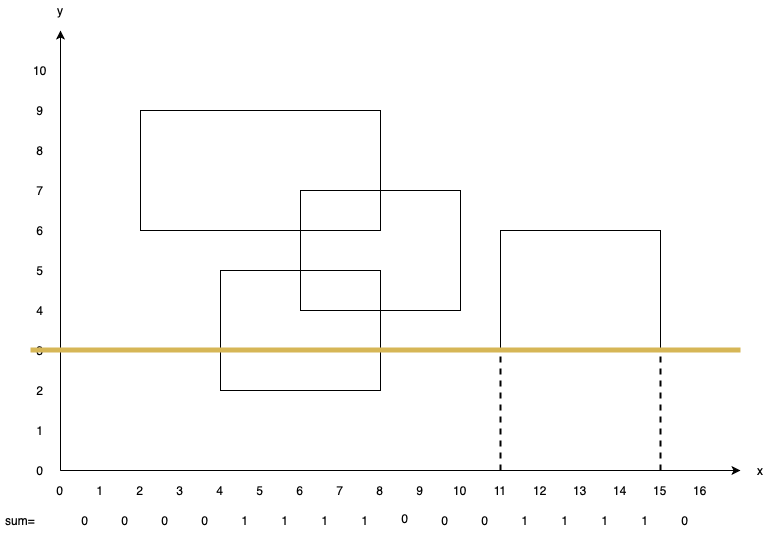
We stop at $y=3$. This time, we first update the answer by adding the area we’ve passed from the previous stopped point i.e. $y=2$. As we can see in the picture, only $sum[4, 5, 6, 7]$ have value greater than $0$. Therefore answer is updated with $4 \times (3 - 2)=4$. Then, we add $1$ to $sum[11, 12, 13, 14]$, as the edge we met is a bottom edge.
Stop at $y=4$. Update ans with $8\times (4-3)=8$ ($8$ values greater than $0$). Add $1$ to $sum[6, 7, 8, 9]$.
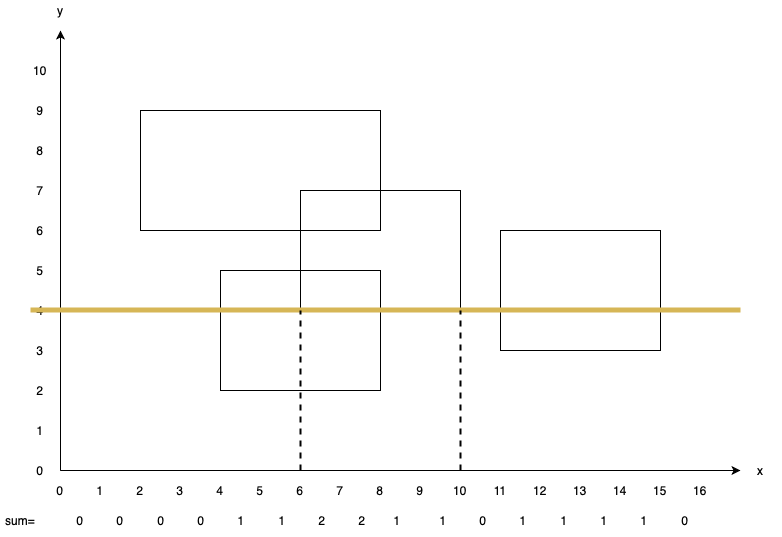
Stop at $y=5$. Update ans with $10\times (5-4)=10$ ($10$ values greater than $0$). As we met a upper edge, add $-1$ to $sum[4, 5, 6, 7]$.
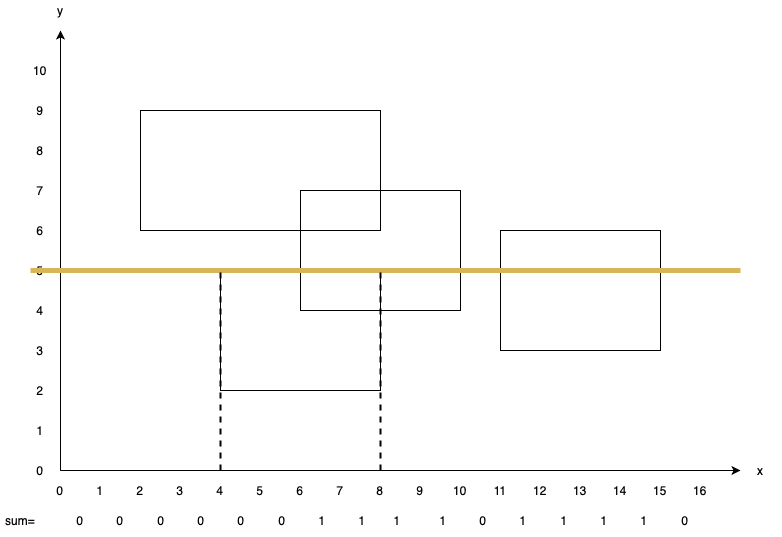
Stop at $y=6$. Update ans with $8\times (6-5)=8$ ($8$ values greater than $0$). Add $1$ to $sum[2, 3, 4, 5, 6, 7]$ and $-1$ to $sum[11, 12, 13, 14]$.
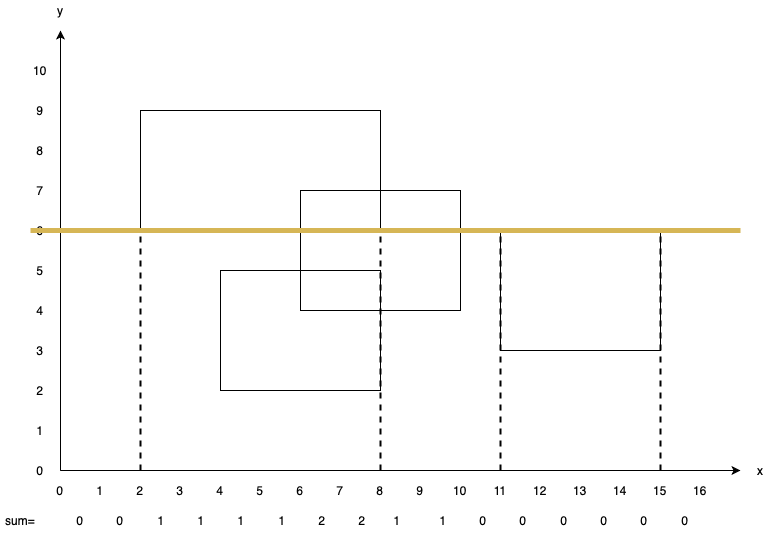
Stop at $y=7$. Update ans with $8\times (7-6)=8$ ($8$ values greater than $0$). Add $-1$ to $sum[6, 7, 8, 9]$.
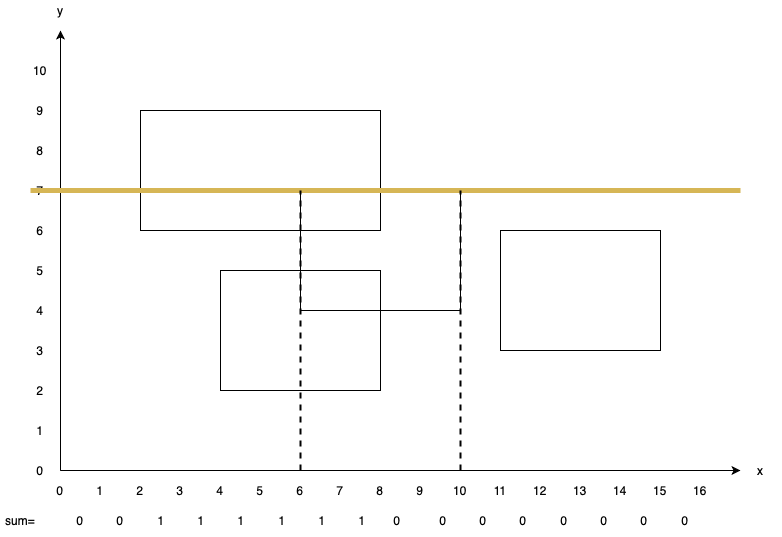
Stop at $y=9$. Update ans with $6\times (9-7)=12$ ($6$ values greater than $0$). Add $-1$ to $sum[2, 3, 4, 5, 6, 7]$.
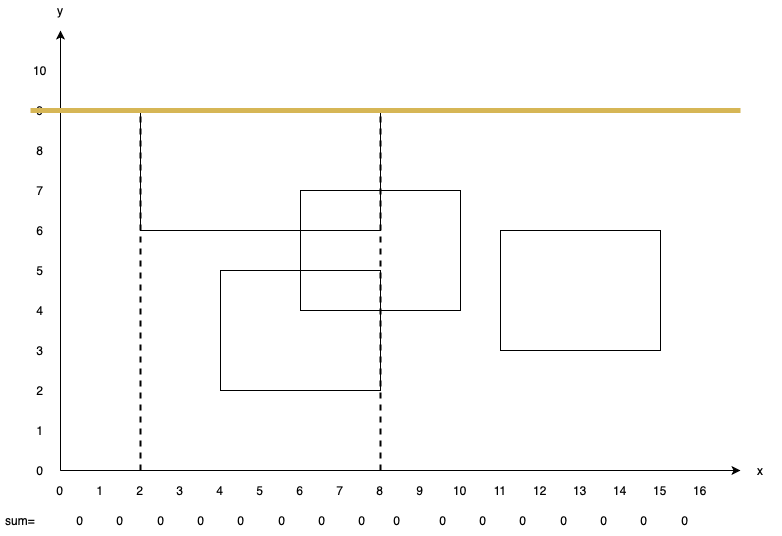
So the final answer is $50$.
Problem solution
For implementation, we need to maintain a segment tree that can tell us how many values are greater than $0$. How do we do this?
For every node is the segment tree, we maintain two values: $tag$ and $sum$, representing “values added in that interval”(lazy tag) and “numbers of element greater than $0$” respectively. The update rule is given as following:
The time complexity is $O(N\log C)$.
void pull(int l, int r, int o) {
// tag[o] > 0 means that all elements in intervel [l, r) is greater than 0
if(tag[o]) sum[o] = r - l;
// tag[o] = 0 means some elements in this intervel is zero;
// thus, we need to get the value from lson and rson
else sum[o] = (l + 1 == r ? 0 : sum[o * 2 + 1] + sum[o * 2 + 2]);
}
code
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N = (int)1e6 + 5;
namespace segtree {
int sum[N * 4], tag[N * 4];
void pull(int l, int r, int o) {
if(tag[o]) sum[o] = r - l;
else sum[o] = (l + 1 == r ? 0 : sum[o * 2 + 1] + sum[o * 2 + 2]);
}
void modify(int l, int r, int ql, int qr, int v, int o=0) {
if(ql <= l && r <= qr) {
tag[o] += v;
}
else {
int mid = (l + r) >> 1, lson = o * 2 + 1, rson = o * 2 + 2;
if(qr <= mid) modify(l, mid, ql, qr, v, lson);
else if(mid <= ql) modify(mid, r, ql, qr, v, rson);
else {
modify(l, mid, ql, mid, v, lson);
modify(mid, r, mid, qr, v, rson);
}
}
pull(l, r, o);
}
int query() {
return sum[0];
}
}
struct Seg {
int l, r, y, v;
bool operator<(const Seg& rhs) const {
return y < rhs.y;
}
};
int n;
vector<Seg> v;
void init() {
cin >> n;
for(int i = 0 ; i < n ; ++i) {
int l, r, d, u; cin >> l >> r >> d >> u;
v.push_back({l, r, d, 1});
v.push_back({l, r, u, -1});
}
sort(v.begin(), v.end());
}
void solve() {
ll ans = 0, preY = 0;
for(auto [ql, qr, y, val] : v) {
ans += segtree::query() * (y - preY);
segtree::modify(0, 1000000, ql, qr, val);
preY = y;
}
cout << ans << '\n';
}
int main() {
ios_base::sync_with_stdio(0), cin.tie(0);
init();
solve();
}
HDU1255 - Rectangle union area 2 (Chinese)
Problem description
Given $N$ rectangles where every rectangle is described by $(X_1, Y_1, X_2, Y_2)$(floating point numbers), meaning that the top-left corner of the rectangle is $(X_1, Y_1)$ and the bottom-right of the rectangle is $(X_2, Y_2)$, please calculate the total area that has been covered by at least two different rectangles.
There are $T$ testcases in a testdata.
$1\le T \le 100, 1\le N\le 10^3, 0\le X_1, Y_1, X_2, Y_2 \le 10^5$
Problem analysis
Similar to the previous problem, we can sweep a line and maintain some values in the segment tree to solve it. However, two values are not enough in this problem. Therefore, we use three values(?) to solve it.
Problem solution
For every node is the segment tree, we maintain two values: $tag$, $sum$ and $sum2$, representing “values added in that interval”(lazy tag), “number of element greater than $0$” and “number of element greater than $1$” respectively. The update rule is given as following:
void pull(int l, int r, int o) {
int lson = o * 2 + 1, rson = o * 2 + 2;
// Update sum: This part is same as the previous problem
if(tag[o]) sum[o] = x[r] - x[l];
else sum[o] = (l + 1 == r ? 0 : sum[lson] + sum[rson]);
// Update sum2
// tag[o] > 1 means that all elements in intervel [l, r) is greater than 1
if(tag[o] > 1) sum2[o] = x[r] - x[l];
else if(l + 1 == r) sum2[o] = 0; // special case
// tag[o] = 1 means that all elements in intervel [l, r) is greater than 0,
// but some elements may be 1; thus, sum2[o] = sum[lson] + sum[rson]
// as if a element is added in lson/rson and added in this node, then its sum is greater than 1
else if(tag[o]) sum2[o] = sum[lson] + sum[rson];
// similarly, tag[o] = 0 means that we need to get the value from sum2[lson] and sum2[rson]
else sum2[o] = sum2[lson] + sum2[rson];
}
The time complexity is $O(N\log C)$.
code
#include <iostream>
#include <algorithm>
#include <vector>
#include <iomanip>
#include <cmath>
using namespace std;
typedef long long ll;
typedef double ld;
struct Seg {
ld l, r, y, v;
bool operator<(const Seg& rhs) const {
return y < rhs.y;
}
};
const int N = (int)2e3 + 5;
const ld eps = 1e-15;
int n;
vector<ld> x;
vector<Seg> v;
namespace segtree {
ld sum[N * 4], sum2[N * 4];
int tag[N * 4];
void init(int n) {
fill(sum, sum + N * 4, 0);
fill(sum2, sum2 + N * 4, 0);
fill(tag, tag + N * 4, 0);
}
void pull(int l, int r, int o) {
int lson = o * 2 + 1, rson = o * 2 + 2;
if(tag[o] > 1) sum2[o] = x[r] - x[l];
else if(l + 1 == r) sum2[o] = 0;
else if(tag[o]) sum2[o] = sum[lson] + sum[rson];
else sum2[o] = sum2[lson] + sum2[rson];
if(tag[o]) sum[o] = x[r] - x[l];
else sum[o] = (l + 1 == r ? 0 : sum[lson] + sum[rson]);
}
void modify(int l, int r, int ql, int qr, int v, int o=0) {
if(ql <= l && r <= qr) {
tag[o] += v;
}
else {
int mid = (l + r) >> 1, lson = o * 2 + 1, rson = o * 2 + 2;
if(qr <= mid) modify(l, mid, ql, qr, v, lson);
else if(mid <= ql) modify(mid, r, ql, qr, v, rson);
else {
modify(l, mid, ql, mid, v, lson);
modify(mid, r, mid, qr, v, rson);
}
}
pull(l, r, o);
}
ld query() {
return sum2[0];
}
}
int id(ld d) {
return lower_bound(x.begin(), x.end(), d) - x.begin();
}
void init() {
cin >> n; v.clear(); x.clear();
for(int i = 0 ; i < n ; ++i) {
ld l, d, r, u; cin >> l >> d >> r >> u;
v.push_back({l, r, d, 1});
v.push_back({l, r, u, -1});
x.push_back(l);
x.push_back(r);
}
sort(x.begin(), x.end());
x.resize(unique(x.begin(), x.end()) - x.begin());
n = (int)x.size();
sort(v.begin(), v.end());
for(auto &i : v) {
i.l = id(i.l), i.r = id(i.r);
}
}
void solve() {
ld ans = 0, preY = 0;
segtree::init(n);
for(auto i : v) {
ans += segtree::query() * (i.y - preY);
segtree::modify(0, n, i.l, i.r, i.v);
preY = i.y;
}
cout << fixed << setprecision(2) << ans + eps << '\n';
}
int main() {
ios_base::sync_with_stdio(0), cin.tie(0);
int t; cin >> t;
while(t--) {
init();
solve();
}
}
IOI ’98 - Picture
Problem description
Given $N$ rectangles where every rectangle is described by $(X_1, Y_1, X_2, Y_2)$, meaning that the bottom-left corner of the rectangle is $(X_1, Y_1)$ and the top-right of the rectangle is $(X_2, Y_2)$, please calculate the union perimeter of those $N$ rectangles.
$0\le N\le 5\times 10^3, -10^4\le X_1, Y_1, X_2, Y_2\le 10^4$
Problem analysis
Still, we sweep over the rectangles like above. However, this time we need to maintain a different information: number of (not connected) segments and total lenght of those segments. The second one same as above, but can the first one be done with segment trees?
Yes! (of course otherwise I won’t mention this problem here :p). We maintain several informations including $lp$ (position of the leftmost element that’s greater than $0$), $rp$ (position of the rightmost element that’s greater than $0$). Then, we’re good to go.
Problem solution
These are Informations needed to maintain:
- $sum$ : number of segments in this interval
- $len$ : number of elements greater than $0$ in this interval
- $tag$ : lazy tag
- $lp$ : position of the leftmost element that’s greater than $0$
- $rp$ : position of the rightmost element that’s greater than $0$
The update rules are:
void pull(int l, int r, int o) {
// tag[o] > 0 means that all elements in this interval is > 0
if(tag[o]) sum[o] = lp[o] = rp[o] = 1, len[o] = r - l;
else if(l + 1 == r) sum[o] = len[o] = lp[o] = rp[o] = 0;
else {
int lson = o * 2 + 1, rson = o * 2 + 2;
sum[o] = sum[lson] + sum[rson] - (rp[lson] && lp[rson]);
len[o] = len[lson] + len[rson];
lp[o] = lp[lson], rp[o] = rp[rson];
}
}
The time complexity is again $O(N\log C)$.
code
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N = 10000 + 5;
namespace segtree {
int sum[N * 8], len[N * 8], tag[N * 8];
bool lp[N * 8], rp[N * 8];
void pull(int l, int r, int o) {
if(tag[o]) sum[o] = lp[o] = rp[o] = 1, len[o] = r - l;
else if(l + 1 == r) sum[o] = len[o] = lp[o] = rp[o] = 0;
else {
int lson = o * 2 + 1, rson = o * 2 + 2;
sum[o] = sum[lson] + sum[rson] - (rp[lson] && lp[rson]);
len[o] = len[lson] + len[rson];
lp[o] = lp[lson], rp[o] = rp[rson];
}
}
void modify(int l, int r, int ql, int qr, int v, int o=0) {
if(ql <= l && r <= qr) {
tag[o] += v;
}
else {
int mid = (l + r) >> 1, lson = o * 2 + 1, rson = o * 2 + 2;
if(qr <= mid) modify(l, mid, ql, qr, v, lson);
else if(mid <= ql) modify(mid, r, ql, qr, v, rson);
else {
modify(l, mid, ql, mid, v, lson);
modify(mid, r, mid, qr, v, rson);
}
}
pull(l, r, o);
}
int qsum() {
return sum[0];
}
int qlen() {
return len[0];
}
}
struct Seg {
int l, r, y, v;
bool operator<(const Seg& rhs) const {
return y < rhs.y;
}
};
int n;
vector<Seg> v;
void init() {
cin >> n;
for(int i = 0 ; i < n ; ++i) {
int l, d, r, u; cin >> l >> d >> r >> u;
v.push_back({l, r, d, 1});
v.push_back({l, r, u, -1});
}
sort(v.begin(), v.end());
}
void solve() {
int ans = 0, preY = 0;
for(auto i : v) {
ans += segtree::qsum() * 2 * (i.y - preY);
int tt = segtree::qlen();
segtree::modify(-N, N, i.l, i.r, i.v);
ans += abs(tt - segtree::qlen());
preY = i.y;
}
cout << ans << '\n';
}
int main() {
ios_base::sync_with_stdio(0), cin.tie(0);
init();
solve();
}