A Simple Introduction to Li-Chao Segment Tree
tags:icpc
algorithm
segment-tree
convex-hull-trick
Log
- [Updated on 2023-01-16: Fix Problem Analysis of “Codechef - Polynomials”]
Outline
What is Li-Chao Segment Tree?
Basically, Li-Chao Segment Trees can solve problems like this:
You’re given a set $S$ containing function of the same “type” (ex. lines, $y=ax+b$). The type of function need to have the transcending property (will be explained later). You need to handle two type of queries:
- Add a function to $S$
- Answer the maximum/minimum value at $x=t$ considering all functions in $S$
A type of function has transcending property if:
Given two functions $f(x), g(x)$ of that type, if $f(t)$ is greater than/smaller than $g(t)$ for some $x=t$, then $f(x)$ will be greater than/smaller than $g(x)$ for $x>t$. In other words, once $f(x)$ “win/lose” $g(x)$, $f(x)$ will continue to “win/lose” $g(x)$.
Implementation
We use line as an example here:
struct Line {
ld m, b;
ld operator()(ld x) { return m * x + b; }
} a[C * 4];
On every node of the segment tree, we store the line that maximize(or minimize) the value of the middle i.e. if the interval of the node is $[L, R)$ , then the line stored on it maximize(or minimize) $\frac{L+R}{2}$.
Insert
Suppose that we are inserting a new line to the node which corresponding interval is $[L, R)$. For conveinence, we assume that the line on the node have a smaller slope. Let $mid=\frac{L+R}{2}$. Then, we have two cases to consider ($red$ is the original line in the node):
- $red(mid) < blue(mid)$
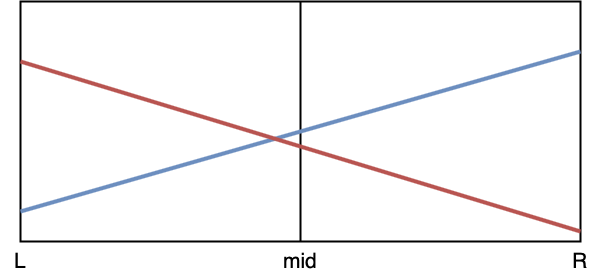
In this case, we should replace $red$ with $blue$. But should we discard $red$? No! As you can see, somewhere in $[L, mid)$ needs $red$. Therefore, we should pass this line to the node with interval $[L, mid)$, which is its left son.
- $red(mid) > blue(mid)$
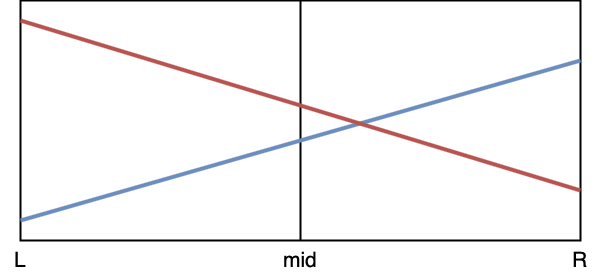
Similarly, we should keep $red$ in this node and pass $blue$ to its right son, whose corresponding interval is $[mid, R)$.
void insert(int l, int r, Line seg, int o=0) {
if(l + 1 == r) {
if(seg(l) > a[o](l)) a[o] = seg;
return;
}
int mid= (l + r) >> 1, lson = o * 2 + 1, rson = o * 2 + 2;
if(a[o].m > seg.m) swap(a[o], seg);
if(a[o](mid) < seg(mid)) {
swap(a[o], seg);
insert(l, mid, seg, lson);
}
else insert(mid, r, seg, rson);
}
The time complexity is $O(\log C)$, where $C$ is the size of range we maintain.
Query
From the way we insert lines, we know that we only need to consider intervals that conatins the point we want to ask.
ld query(int l, int r, int x, int o=0) {
if(l + 1 == r) return a[o](x);
int mid = (l + r) >> 1, lson = o * 2 + 1, rson = o * 2 + 2;
if(x < mid) return max(a[o](x), query(l, mid, x, lson));
else return max(a[o](x), query(mid, r, x, rson));
}
The time complexity is still $O(\log C)$, as we will only pass $O(\log C)$ nodes.
Example problems
BZOJ1568 - Blue Mary’s Company
Problem description
You have a empty set of lines $S$ in the beginning. You need to handle $Q$ queries of two kinds:
- $Project\space a\space b$ : Insert a line $f(x)=bx+(a-b)$.
- $Query\space t$ : Calculate $\max_{f\in S} \left\{ f(t) \right\}$
$1\le Q\le 10^5, 1\le T \le 5\times 10^4, |a| \le 10^6, 0 < b < 100$
Problem analysis
You might discover that this problem can be solved with dynamic hull, and commonly used dynamic hull algorithm has $O(N\log N)$ complexity, where $N$ is the number of lines. However, dynamic hull is usually hard to implement and have a large constant factor in practice. So, let’s solve this problem using Li-Chao segment tree! Observe that “line” is a function type that have the transcending property, thus we can use Li-Chao segment tree.
Problem solution
This problem can be solved almost directly by the code above. Please kindly refer to the code for more details. The complexity is $O(Q\log T)$ .
code
#include <iostream>
using namespace std;
typedef long long ll;
typedef long double ld;
const int C = (int)5e4 + 5;
namespace segtree {
struct Line {
ld m, b;
ld operator()(ld x) { return m * x + b; }
} a[C * 4];
void insert(int l, int r, Line seg, int o=0) {
if(l + 1 == r) {
if(seg(l) > a[o](l)) a[o] = seg;
return;
}
int mid= (l + r) >> 1, lson = o * 2 + 1, rson = o * 2 + 2;
if(a[o].m > seg.m) swap(a[o], seg);
if(a[o](mid) < seg(mid)) {
swap(a[o], seg);
insert(l, mid, seg, lson);
}
else insert(mid, r, seg, rson);
}
ld query(int l, int r, int x, int o=0) {
if(l + 1 == r) return a[o](x);
int mid = (l + r) >> 1, lson = o * 2 + 1, rson = o * 2 + 2;
if(x < mid) return max(a[o](x), query(l, mid, x, lson));
else return max(a[o](x), query(mid, r, x, rson));
}
}
void init() {
}
void solve() {
int q; cin >> q;
while(q--) {
string s; cin >> s;
if(s[0] == 'P') {
ld b, m; cin >> b >> m;
segtree::insert(1, C, {m, b - m});
}
else {
int x; cin >> x;
cout << (int)(segtree::query(1, C, x) / 100) << '\n';
}
}
}
int main() {
ios_base::sync_with_stdio(0);
init();
solve();
}
Codechef - Polynomials
Problem description
You’re given $N$ functions $y_i(x)=a_0 + a_1x + a_2x^2 + a_3x^3$. Now, you need to answer $Q$ queries. For every query, you are given an integer $t$ and you need to answer $\min_{1\le i\le N}\left\{ y_i(t) \right\}$ .
$1\le N, Q\le 10^5, 0\le t\le 10^5, 0\le a_3\le 10^3, 0\le a_0, a_1, a_2\le 10^5$
Problem analysis
First, notice that the range of query is $[0, 10^5]$. Then, it can be prove that after $sqrt(10^5)$ (maximum value of $t$), two functions can intersect at most one time. Therefore, we can maintain $x=[0, sqrt(10^5)]$ directly and maintain $x=[sqrt(10^5)+1, 10^5]$ using li-chao segment trees.
Problem solution
The solution is described above. Note that we do not use slope to decide which function to pass down, but uses the value of $x=L$ and $x=mid$. Refer to the code for more details. The time complexity is $O((N+Q)\log C)$.
code
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N = (int)1e5 + 5;
const int C = (int)1e5 + 5;
const int T = 10;
const int M = 350; // sqrt(10^5)
const ll inf = (ll)1e19;
namespace segtree {
struct Poly {
ll a, b, c, d = inf;
ll operator()(ll x) { return a * x * x * x + b * x * x + c * x + d; }
} a[T][C * 4];
int t = -1;
void insert(int l, int r, Poly poly, int o=0) {
if(l + 1 == r) {
if(poly(l) < a[t][o](l)) a[t][o] = poly;
return;
}
int mid = (l + r) >> 1, lson = o * 2 + 1, rson = o * 2 + 2;
bool b1 = poly(mid) < a[t][o](mid), b2 = poly(l) < a[t][o](l);
if(b1) swap(poly, a[t][o]);
if(b1 != b2) insert(l, mid, poly, lson);
else insert(mid, r, poly, rson);
}
ll query(int l, int r, int x, int o=0) {
if(l + 1 == r) return a[t][o](x);
int mid = (l + r) >> 1, lson = o * 2 + 1, rson = o * 2 + 2;
if(x < mid) return min(a[t][o](x), query(l, mid, x, lson));
else return min(a[t][o](x), query(mid, r, x, rson));
}
}
ll ans[M];
void init() {
int n; cin >> n;
fill(ans, ans + M, inf);
segtree::t++;
while(n--) {
int a, b, c, d; cin >> d >> c >> b >> a;
segtree::Poly p = {a, b, c, d};
segtree::insert(M, C, p);
for(int i = 0 ; i < M ; ++i) ans[i] = min(ans[i], p(i));
}
}
void solve() {
int q; cin >> q;
while(q--) {
int x; cin >> x;
if(x < M) cout << ans[x] << '\n';
else cout << segtree::query(M, C, x) << '\n';
}
}
int main() {
ios_base::sync_with_stdio(0), cin.tie(0);
int t; cin >> t;
while(t--) {
init();
solve();
}
}
CF923F - Escape Through Leaf
Problem description
You’re given a tree with $n$ nodes rooted at node $1$. Each node has two associated value $a_i, b_i$. You can jump from a node to any node in its subtree. The cost of jump from node $u$ to $v$ is $a_u\times b_v$. Note that you cannot jump from a node to itself.
Now, you need to calculate the minimum cost to reach leaf for every node. Node that node $1$ is not considered a leaf even it’s degree is $1$.
$1\le N\le 2\times 10^5, |a_i|, |b_i| \le 10^5$
Problem analysis
First, that this problem is a DP problem with the transition equation be: $$ dp_u = \max_{v\in subtree_u} \left\{ dp_v + a_u \times b_v \right\} $$ Then, observe that $dp_v + a_u \times b_v$ can be viewed as lines $b_v\times x + dp_v$, which means that what we are finding is the maximum value of $x=a_u$ among all lines formed by nodes in its subtree. This can be done by li-chao segment tree, obviously.
Thus, we can build a li-chao segment tree for every node and merge it to its parent. If we always merge the small ones to the big ones, then the number of extra inserts will only be $O(N\log N)$.
Problem solution
The solution is described above. We implemented li-chao segment tree with dynamic node creation. More details in code. The time complexity is $O(N\log N\log C + N\log C)$, and the space complexity is $O(N)$(we have only $N$ lines).
code
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int C = (int)1e5 + 5;
const int N = (int)1e5 + 5;
const ll inf = (ll)1e18;
struct Line {
ll m, b;
ll operator()(ll x) { return m * x + b; }
};
struct Node {
Line seg;
Node *lson, *rson;
Node(Line _seg): seg(_seg), lson(0), rson(0) {}
};
void insert(int l, int r, Line seg, Node* o) {
if(l + 1 == r) {
if(seg(l) < o->seg(l)) o->seg = seg;
return;
}
int mid = (l + r) >> 1;
if(seg.m < o->seg.m) swap(seg, o->seg);
if(o->seg(mid) > seg(mid)) {
swap(seg, o->seg);
if(o->rson) insert(mid, r, seg, o->rson);
else o->rson = new Node(seg);
}
else {
if(o->lson) insert(l, mid, seg, o->lson);
else o->lson = new Node(seg);
}
}
ll query(int l, int r, int x, Node* o) {
if(l + 1 == r) return o->seg(x);
int mid = (l + r) >> 1;
if(x < mid && o->lson) return min(o->seg(x), query(l, mid, x, o->lson));
else if(o->rson) return min(o->seg(x), query(mid, r, x, o->rson));
return o->seg(x);
}
void del(Node* o) {
if(o->lson) del(o->lson);
if(o->rson) del(o->rson);
delete o;
}
void merge(Node* dest, Node* o) {
if(o->seg.m != 0 || o->seg.b != inf) insert(-C, C, o->seg, dest);
if(o->lson) merge(dest, o->lson);
if(o->rson) merge(dest, o->rson);
}
ll n, a[N], b[N], dp[N];
vector<int> G[N];
pair<int, Node*> dfs(int u, int p) {
int sz = 0; Node* root = new Node({0, inf});
for(auto v : G[u]) if(v != p) {
auto [szz, son] = dfs(v, u);
if(sz < szz) swap(root, son);
merge(root, son);
del(son);
sz += szz;
}
dp[u] = (sz ? query(-C, C, a[u], root) : 0);
insert(-C, C, {b[u], dp[u]}, root);
return {sz + 1, root};
}
void init() {
cin >> n;
for(int i = 1 ; i <= n ; ++i) cin >> a[i];
for(int i = 1 ; i <= n ; ++i) cin >> b[i];
for(int i = 1 ; i < n ; ++i) {
int u, v; cin >> u >> v;
G[u].push_back(v);
G[v].push_back(u);
}
}
void solve() {
dfs(1, 0);
for(int i = 1 ; i <= n ; ++i) cout << dp[i] << ' ';
cout << '\n';
}
int main() {
ios_base::sync_with_stdio(0), cin.tie(0);
init();
solve();
}