A Simple Introduction to Fenwick Trees (Binary Indexed Tree, BIT)
tags:icpc
algorithm
fenwick-tree
Outline
What’s a Fenwick Tree?
A Fenwick Tree or binary indexed tree(BIT) is a data structure that can efficiently ($O(\log N)$, where $N$ is the length of table) update elements and calculate prefix sums in a table of numbers. - Wikipedia
First, we define $lowbit$ operation: $lowbit(i)$ returns the value of rightmost $1$ in binary representation of $i$. For example,
- $lowbit((13)_{10})=lowbit((1101)_2)=1$
- $lowbit((12)_{10})=lowbit((1101)_2)=4$
In most computers, this operation can be done with $lowbit(i)=i \& (-i)$ as most computers store negetive number with its complement.
1-Dimension BIT
Suppose that we have a array $A=A_1, A_2, \dots, A_{15}$ with length $15$. Then, its BIT looks like this:
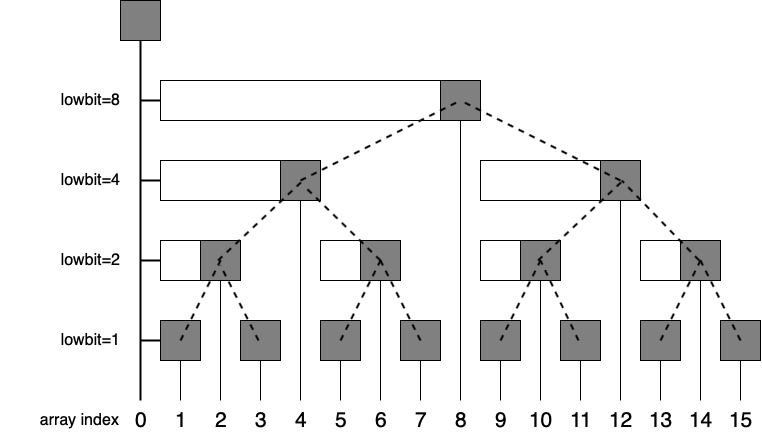
From the picture above, we can observe that:
- We can store BIT in a normal array. Let’s call it $B$.
- $B_i=\sum\limits_{j=i-lowBIT(i)+1}^{i}A_j$. In other words, $B_i$ represents the sum of elements whose index belongs to $[i-lowBIT(i)+1, i]$, which is a segment ending at $i$ and has length $lowBIT(i)$.
Update
Now suppose that we want to update $A_5$ to a new value. Then, we need to update nodes with brown color:
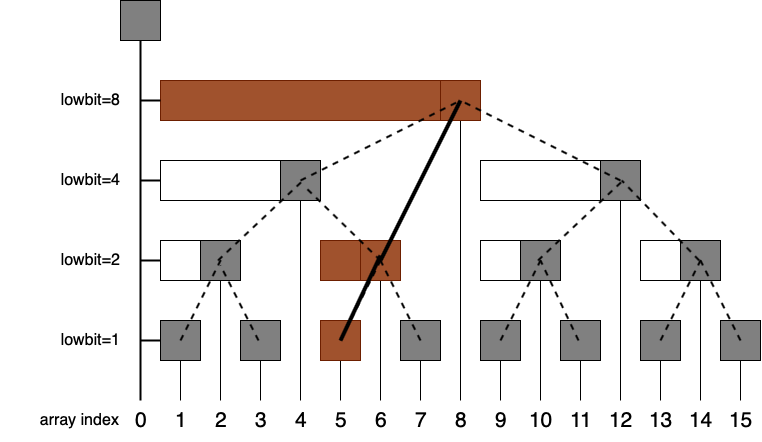
Observe that the relationship between set of brown nodes with $5$ is that $5+lowBIT(5)=6$, $6+lowBIT(6)=8$.
So now we know what to do when updating an element $A_i$: “crawling up-right” the BIT and update each node. As the height of BIT is $O(\log N)$, the complexity for update is $O(\log N)$.
Query
Now suppose that we want to query prefix sum that endes at $A_{13}$. Then, we need to add values stored at nodes with brown color:
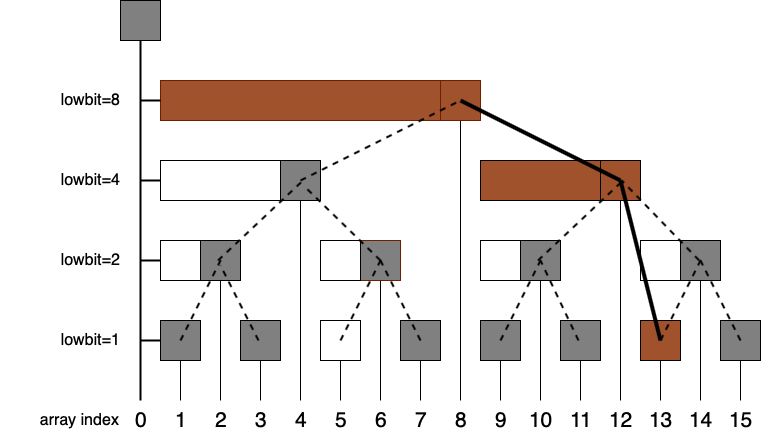
Observe that the relationship between set of brown nodes with $13$ is that $13-lowBIT(13)=12$, $12+lowBIT(12)=8$.
So now we know what to do when calculating prefix sum ending at $A_i$: “crawling up-left” the BIT and add each node’s value to the answer. As the height of BIT is $O(\log N)$, the complexity for query is $O(\log N)$.
2-Dimension BIT
Recall that in 1D BIT, $i^{th}$ element in BIT store the sum of interval ending at $i$ with length $lowbit(i)$. Similarly, in 2D BIT, the $(i, j)^{th}$ element store the sum of rectangle ending(right-bottom point) at point $(i, j)$ with height $lowbit(i)$ and weight $lowbit(i)$. Below is a picture illustrating the BIT in case $N=3, M=3$.
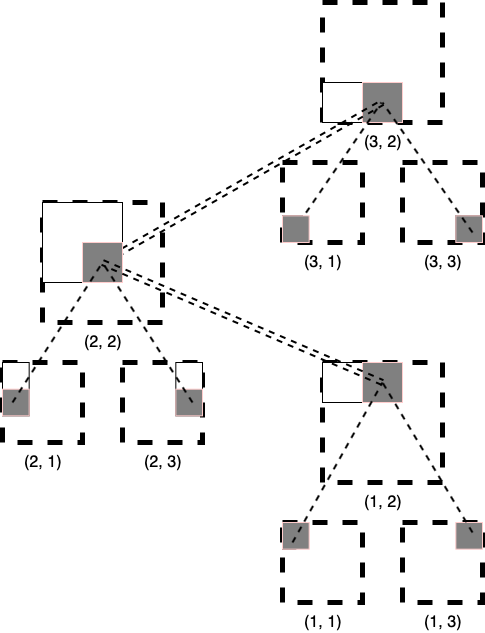
The complexity for both update and query are $O(\log^2 N)$.
Some problems
BIT is usually used as a tool to solve problems, rather than being the main part of the solution. So, I only choose classic problems(and their variations) here. All of the following problems have the same template: point/range update values(addition), point/range query interval sums(addition).
1D Point update, Range query
Classic BIT application:
int A[N], B[N], n;
void upd(int x, int v) {
for(int i = x ; i <= n ; i += lowbit(i)) B[i] += v;
}
int sum(int x) {
int ans = 0;
for(int i = x ; i > 0 ; i -= lowbit(i)) ans += B[i];
return ans;
}
int query(int l, int r) {
return sum(r) - sum(l - 1);
}
void init() {
fill(B, B + n + 1, 0);
for(int i = 1 ; i <= n ; ++i) upd(i, A[i]);
}
1D Range update, Point query
Of course, we can view a range update as several point updates. However, this will make the time complexity of update degrade to $O(N\log N)$.
Can we do it better? Yes!
Given array $A=A_1, A_2, \dots, A_N$, we construct a difference array $D=D_1, D_2, \dots, D_N$, where $D_i=A_i-A_{i-1}$, and $A_0=0$.
Observe that $A_i=\sum\limits_{j=1}^{i}D_i$, which is exactly the prefix sum of $D$. Thus, we have a solution now:
- Update $(l, r)$ with $v$: Update $D_{r+1}$ with $-v$ and $D_l$ with $v$.
- Query $i$: return prefix sum of $D$ ending at $i$.
int A[N], B[N], n;
void upd(int x, int v) {
for(int i = x ; i <= n ; i += lowbit(i)) B[i] += v;
}
int sum(int x) {
int ans = 0;
for(int i = x ; i > 0 ; i -= lowbit(i)) ans += B[i];
return ans;
}
void update(int l, int r, int v) {
upd(r + 1, -v); upd(l, v);
}
void init() {
fill(B, B + n + 1, 0); A[0] = 0;
for(int i = 1 ; i <= n ; ++i) upd(i, A[i] - A[i - 1]);
}
1D Range update, Range query
This one is trickier. Similar to the previous problem, we first create a difference array $D$. Then, observe that prefix sum of $A$ ending at $i$ is $$ \sum_{j=1}^{i}A_j= \sum_{j=1}^{i}\sum_{k=1}^{j}D_k=iD_1+(i-1)D_2+\dots=(i+1)\sum_{j=1}^{i}D_j-\sum_{j=1}^{i}jD_j $$ We can maintain the two prefix sums, $D_i$ and $iD_i$, with two BIT.
int A[N], B1[N], B2[N], n;
void upd(int* B, int x, int v) {
for(int i = x ; i <= n ; i += lowbit(i)) B[i] += v;
}
int sum(int* B, int x) {
int ans = 0;
for(int i = x ; i > 0 ; i -= lowbit(i)) ans += B[i];
return ans;
}
void update(int l, int r, int v) {
upd(B1, r + 1, -v); upd(B1, l, v);
upd(B2, r + 1, -(r + 1) * v); upd(B2, l, l * v);
}
int query(int l, int r) {
return ((r + 1) * sum(B1, r) - sum(B2, r)) - (l * sum(B1, l - 1) - sum(B2, l - 1));
}
void init() {
A[0] = 0;
fill(B1, B1 + n + 1, 0);
fill(B2, B2 + n + 1, 0);
for(int i = 1 ; i <= n ; ++i) upd(i, A[i] - A[i - 1]);
}
2D Point update, Range query
Classic 2D BIT application. See code for more details.
int A[N][N], B[N][N], n, m;
void upd(int x, int y, int v) {
for(int i = x ; i <= n ; i += lowbit(i)) {
for(int j = y ; j <= m ; j += lowbit(j)) {
B[i][j] += v;
}
}
}
int sum(int x, int y) {
int ans = 0;
for(int i = x ; i > 0 ; i -= lowbit(i)) {
for(int j = y ; j > 0 ; j -= lowbit(j)) {
ans += B[i][j];
}
}
return ans;
}
int query(int x1, int y1, int x2, int y2) {
return sum(x2, y2) - sum(x1 - 1, y2) - sum(x2, y1 - 1) + sum(x1 - 1, y1 - 1);
}
void init() {
memset(B, 0, sizeof(B));
for(int i = 1 ; i <= n ; ++i) {
for(int j = 1 ; j <= m ; ++j) {
upd(i, j, A[i][j]);
}
}
}
2D Range update, Point query
Recall that in problem “1D Range update, Point query”, we created a difference array $D$ to help us. Can we do the similar thing here? Let’s try it.
Note that prefix sum of $A$ ending at $(i, j)$ is $prefix_{i-1, j}+prefix_{i, j-1}-prefix_{i-1, j-1}+A_{i, j}$.
Therefore, we can define $D_{i, j}$ as $A_{i, j} - A_{i-1, j} - A_{i, j-1} + A_{i-1, j-1}$, and $A_{i, j}=\sum\limits_{k=1}^{i}\sum\limits_{l=1}^{j}D_{k, l}$.
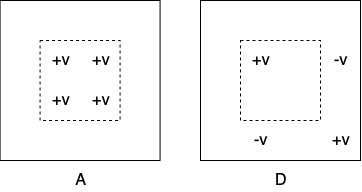
When we update $(x1, y1, x2, y2)$ with $v$, four values in $D$ will change:
- $D_{x2+1, y2+1}$ increase by $v$
- $D_{x1, y1}$ increase by $v$
- $D_{x2+1, y1}$ decrease by $v$
- $D_{x1, y2+1}$ decrease by $v$
If you’re still not clear, the following picture might help:
int A[N][N], B[N][N], n, m;
void upd(int x, int y, int v) {
for(int i = x ; i <= n ; i += lowbit(i)) {
for(int j = y ; j <= m ; j += lowbit(j)) {
B[i][j] += v;
}
}
}
int sum(int x, int y) {
int ans = 0;
for(int i = x ; i > 0 ; i -= lowbit(i)) {
for(int j = y ; j > 0 ; j -= lowbit(j)) {
ans += B[i][j];
}
}
return ans;
}
int update(int x1, int y1, int x2, int y2, int v) {
upd(x2 + 1, y2 + 1, v);
upd(x1, y1, v);
upd(x1, y2 + 1, -v);
upd(x2, y1 + 1, -v);
}
void init() {
memset(B, 0, sizeof(B));
for(int i = 1 ; i <= n ; ++i) {
for(int j = 1 ; j <= m ; ++j) {
upd(i, j, A[i][j]);
}
}
}
2D Range update, Range query
Similar to the previous problem, we first create a difference array $D$. Then, observe that prefix sum of $A$ ending at $(i, j)$ is $$ \begin{align} \sum_{k=1}^{i}\sum_{l=1}^{j}A_{i,j} & = \sum_{k=1}^{i}\sum_{l=1}^{j}\sum_{a=1}^{k}\sum_{b=1}^{l}D_{a,b} \\ & = \sum_{k=1}^{i}\sum_{l=1}^{j}(i-k+1)(j-l+1)D_{k, l} \\ & = (i+1)(j+1)\sum_{k=1}^{i}\sum_{l=1}^{j}D_{k,l} - (i+1)\sum_{k=1}^{i}\sum_{l=1}^{j}kD_{k, l} - (j+1)\sum_{k=1}^{i}\sum_{l=1}^{j}lD_{k, l} + \sum_{k=1}^{i}\sum_{l=1}^{j}klD_{k, l} \end{align} $$
We can maintain the four prefix sums, $D_{i,j}, iD_{i,j}, jD_{i,j}, ijD_{i,j}$, with four BIT.
int n, m, A[N][N], B[N][N][4];
void upd(int x, int y, int v) {
for(int i = x ; i <= n ; i += lowbit(i)) {
for(int j = y ; j <= m ; j += lowbit(j)) {
B[i][j][0] += v;
B[i][j][1] += x * v;
B[i][j][2] += y * v;
B[i][j][3] += x * y * v;
}
}
}
int qry(int x, int y) {
int ans = 0;
for(int i = x ; i > 0 ; i -= lowbit(i)) {
for(int j = y ; j > 0 ; j -= lowbit(j)) {
ans += (x + 1) * (y + 1) * B[i][j][0] - (y + 1) * B[i][j][1] - (x + 1) * B[i][j][2] + B[i][j][3];
}
}
return ans;
}
void update(int x1, int y1, int x2, int y2, int v) {
upd(x1, y1, v);
upd(x1, y2 + 1, -v);
upd(x2 + 1, y1, -v);
upd(x2 + 1, y2 + 1, v);
}
int query(int x1, int y1, int x2, int y2) {
return qry(x2, y2) - qry(x1 - 1, y2) - qry(x2, y1 - 1) + qry(x1 - 1, y1 - 1);
}
void init() {
for(int i = 1 ; i <= n ; ++i) {
for(int j = 1 ; j <= m ; ++j) {
upd(i, j, A[i][j]);
}
}
}