A Simple Introduction to Centroid Decomposition
tags:icpc
algorithm
tree
decomposition
centroid-decomposition
divide-and-conquer
Outline
What’s a centroid?
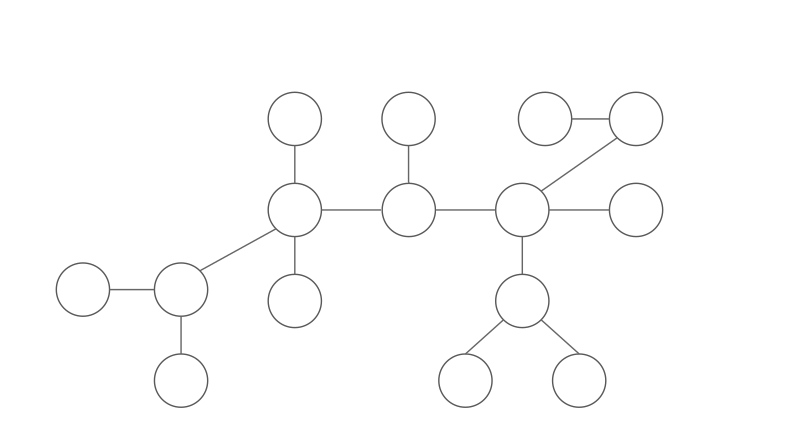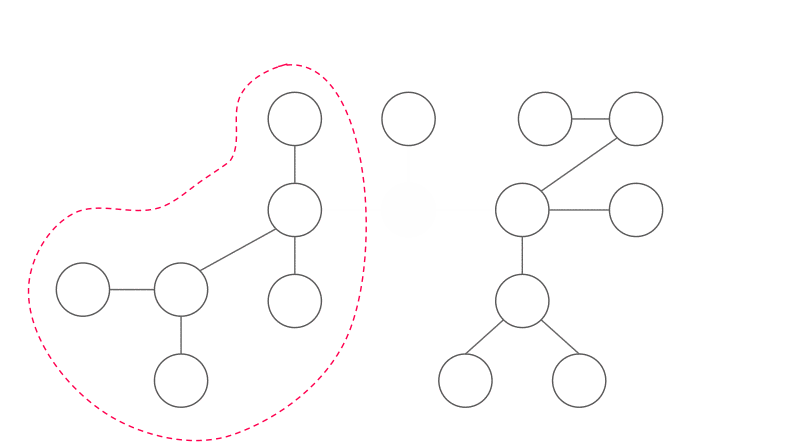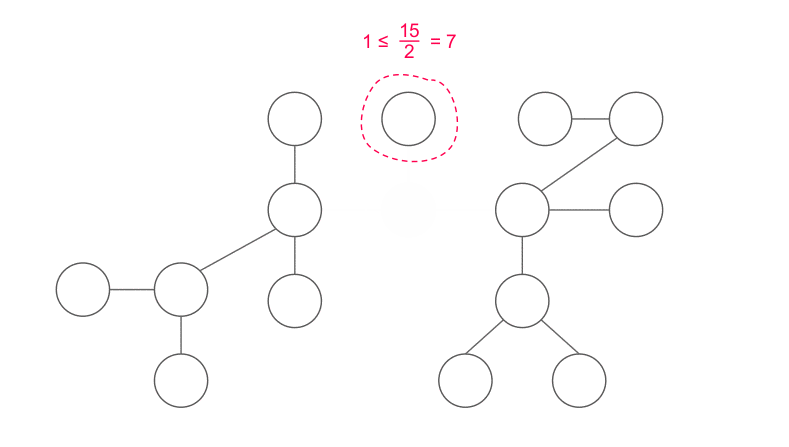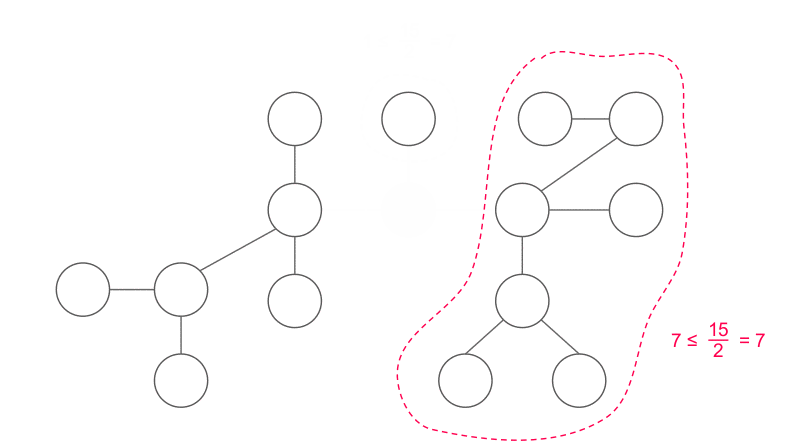
Let $T$ be a tree with $n$ nodes. A node $u$ is a centroid iff the size of each subtree after removing $u$ is not greater than $\frac{n}{2}$. Note that the center of a tree is different from the centroid of a tree, which is usually related with height of the tree. Intuitively, centroid can be viewed as the “center of mass” of $T$.
How to find a centroid?
First, we choose an arbitrary node $x$. We use a DFS to calculate the size of each subtree ($x$ is the root). Then, we can “walk” to the centroid starting from $x$ by:
- If $x$ is the centroid, return $x$.
- Else, we know that exist exactly one node $y$ adjacent to $x$ satisfying $|y| > \frac{n}{2}$. Walk to $y$ and do it again.
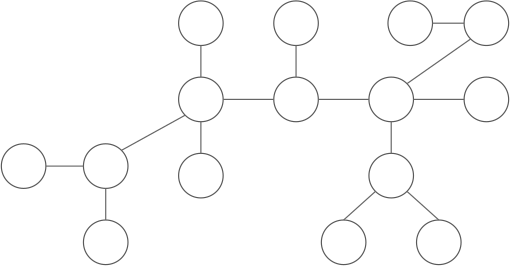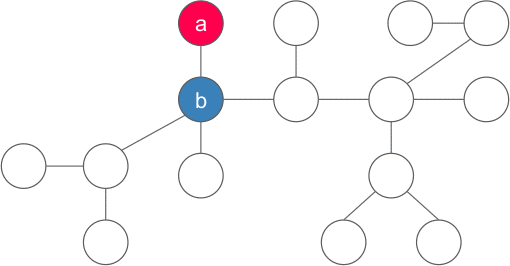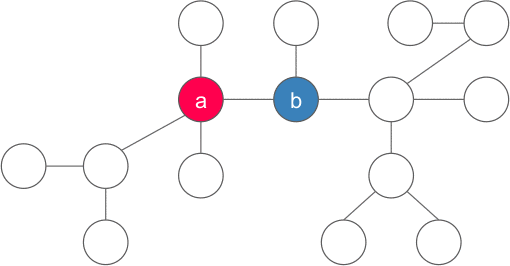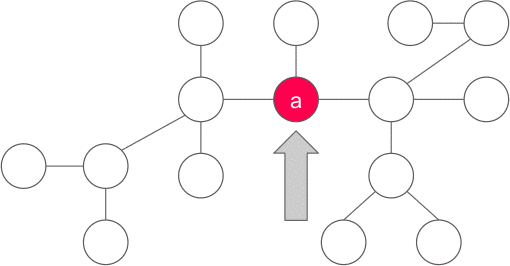
$|y|$ is the number of nodes of the subtree rooted at $y$. Why is there exactly one $y$? There must be at least one such nodes since $x$ is not a centroid, and there must be at most one such nodes since two or more such nodes implies that $|x| > n$ which is impossible.
vector<int> G[N]; // tree stored in adjacency list
int sz[N];
int dfs(int u, int p) {
sz[u] = 1;
for(auto v : G[u]) if(v != p) {
sz[u] += dfs(v, u);
}
return sz[u];
}
int centroid(int u, int p, int n) { // n is the size of tree
for(auto v : G[u]) if(v != p) {
if(sz[v] > n / 2) return centroid(v, u, n);
}
return u;
}
The total complexity is $O(n)$.
Centroid decomposition
This technique is actually Divide and Conquer applied on tree.
What is centroid decomposition?
A centroid decomposition of a tree $T$ is another tree $T^{’}$ defined recursively as:
- root of $T^{’}$ is the centroid of $T$
- childs of the root are the centroid of the subtrees resulting from erasing the centroid of $T$
Too difficult to understand? Let’s see an example:
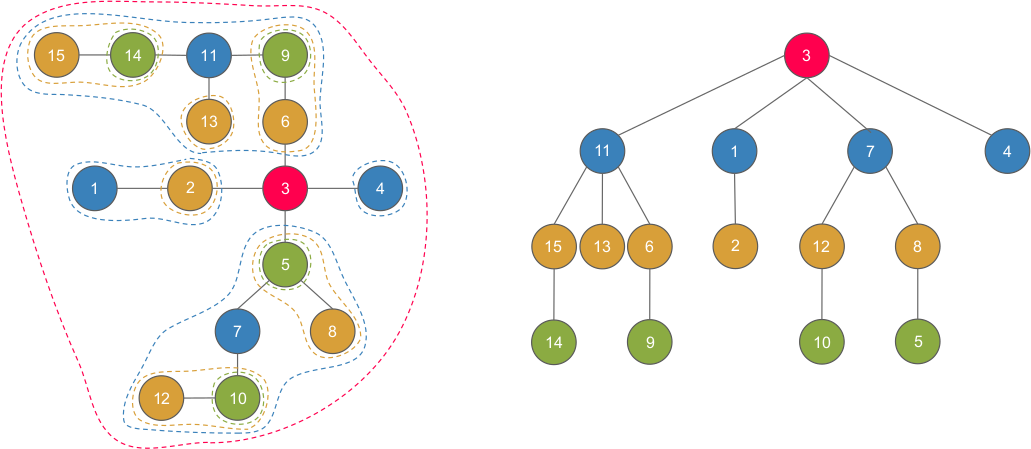
- $3$ is the root of the centroid tree/centroid of the original tree, and $11, 1, 7, 4$ are children of $3$, which are the centroids of the subtrees after removing $3$.
- $11$ is the root of the centroid tree/centroid of the original tree, and $15, 13, 6$ are children of $11$, which are the centroids of the subtrees after removing $11$.
… so on and so on.
Implementation
set<int> G[N]; // adjacency list (note that this is stored in set, not vector)
int sz[N], pa[N];
int dfs(int u, int p) {
sz[u] = 1;
for(auto v : G[u]) if(v != p) {
sz[u] += dfs(v, u);
}
return sz[u];
}
int centroid(int u, int p, int n) {
for(auto v : G[u]) if(v != p) {
if(sz[v] > n / 2) return centroid(v, u, n);
}
return u;
}
void build(int u, int p) {
int n = dfs(u, p);
int c = centroid(u, p, n);
if(p == -1) p = c;
pa[c] = p;
vector<int> tmp(G[c].begin(), G[c].end());
for(auto v : tmp) {
G[c].erase(v); G[v].erase(c);
build(v, c);
}
}
It costs $O(n)$ to build each level of the centroid tree, and the height of the centroid tree is $O(\log n)$. The deletion of edge is also $O(n\log n)$, as we only have $O(n)$ edges to remove and each removal cost $O(\log n)$. Therefore, the total complexity is $O(n\log n)$.
Properties
- A node $u$ belongs to the component of all its ancesters.
- Every path from $u$ to $v$ can be decomposed into path from $u$ to $w$, $w$ to $v$ where $w$ is the least common ancestor of $u$, $v$ in centroid tree.
- We can represent all possible paths in the original tree (there are $n^2$ paths) as a concatenation of two paths in a $O(n\log n)$ set composed of paths like this: $(u, fa(u)), (u, fa(fa(u))), \dots$ for all possible $u$.
If you don’t understand the statement above, the example below might help :)
Example

- Let’s focus on $9$. We can observe that $9$ is in the component of its ancestors $6, 11, 3$.
- Take $14$ to $10$ as an example $\implies$ $path(14,10)=path(14,3)+path(3,10)$, where $3=lca(14,10)$.
- The “$O(n\log n)$ set” contains paths (on the centroid tree) like $(14, 15), (14, 11), (14, 3)$ and $(13, 11), (13, 3)$ and so on. Now we pick an arbitrary path, say $(1, 4)$. Then $(1, 4)=(1, 3)+(4, 3)$, which are both in the given set.
Proofs are given below, click it if you’re interested.
Proof
- Immediate from the construction of centroid tree.
- This can be proved by contradiction. Suppose that $w=lca(u, v)$ is not in the path from $u, v$. This implies that $u, v$ belongs to the same subtree when removing $w$. However, this means that $lca(u, v)$ is not $w\implies $ contradiction.
- First, as the height of centroid tree is $O(\lg n)$, the size of the set is $O(n\lg n)$. Then, by the second property, every path can be decomposed into two parts, splitting at the lca’s. Thus, all possible paths can be represented with elements in that set.
Example problems
CF342E - Xenia and Tree
Problem description
You are given a tree consist of $N$ nodes, indexed from $1$ to $N$. Every node is painted either red or blue. In the beginning, node $1$ is red, and all other nodes are blue. Now, you need to handle $Q$ queries of two kinds:
- $1\space u$: Paint a blue node $u$ into red.
- $2\space u$: Answer the index of the red node closest to $u$.
$2\le N \le 10^5, 1 \le Q \le 10^5$
Problem analysis
First, we can observe that the answer to type $2$ query requires us to consider all paths starting from $u$, which will take $O(N)$ if we do it naively and is unacceptable. Now, take a look at the property 3 of centroid decomposition. This property tells us that if what we want to maintain about a path can be “merged” by two parts of the path, then we can answer type $2$ query in $O(\lg N)$.
Problem solution
For each node $u$, we maintain a value $ans_u=\min\limits_{v\text{ is red, } v\in \text{centroid tree rooted at }u} dis(u, v)$, which is the distance of closest red node to $u$ consider only nodes in component where $u$ is a centroid. Then, we can handle the queries by:
- Paint: update the ans value of all ancestors of $u$ i.e. do $ans_v=\min\left\{ans_v, dis(u, v)\right\}$ for all $v\in \text{ancestors of }u$.
- Query: $\min\limits_{v\in \text{ancestors of} u} \{ans_v + dis(u, v)\}$ is the answer.
Both query take $O(\log N)$, as the depth of centroid tree is at most $O(\log N)$. Thus, the total complexity is $O(Q\log N)$.
code
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N = (int)1e5 + 5;
const int inf = (int)1e9;
struct CentroidDecomposition {
set<int> G[N];
map<int, int> dis[N];
int sz[N], pa[N], ans[N];
void init(int n) {
for(int i = 1 ; i <= n ; ++i) G[i].clear(), dis[i].clear(), ans[i] = inf;
}
void addEdge(int u, int v) {
G[u].insert(v); G[v].insert(u);
}
int dfs(int u, int p) {
sz[u] = 1;
for(auto v : G[u]) if(v != p) {
sz[u] += dfs(v, u);
}
return sz[u];
}
int centroid(int u, int p, int n) {
for(auto v : G[u]) if(v != p) {
if(sz[v] > n / 2) return centroid(v, u, n);
}
return u;
}
void dfs2(int u, int p, int c, int d) { // build distance
dis[c][u] = d;
for(auto v : G[u]) if(v != p) {
dfs2(v, u, c, d + 1);
}
}
void build(int u, int p) {
int n = dfs(u, p);
int c = centroid(u, p, n);
if(p == -1) p = c;
pa[c] = p;
dfs2(c, p, c, 0);
vector<int> tmp(G[c].begin(), G[c].end());
for(auto v : tmp) {
G[c].erase(v); G[v].erase(c);
build(v, c);
}
}
void modify(int u) {
for(int v = u ; v != 0 ; v = pa[v]) ans[v] = min(ans[v], dis[v][u]);
}
int query(int u) {
int mn = inf;
for(int v = u ; v != 0 ; v = pa[v]) mn = min(mn, ans[v] + dis[v][u]);
return mn;
}
} cd;
int n, q;
void init() {
cin >> n >> q;
cd.init(n);
for(int i = 0 ; i < n - 1 ; ++i) {
int a, b; cin >> a >> b; cd.addEdge(a, b);
}
cd.build(1, 0);
}
void solve() {
cd.modify(1);
int t, u;
while(q--) {
cin >> t >> u;
if(t == 1) cd.modify(u);
else cout << cd.query(u) << '\n';
}
}
int main() {
ios_base::sync_with_stdio(0), cin.tie(0);
init();
solve();
}
IOI’11 - Race
Problem description
You are given a weight tree with $N$ nodes, indexed from $1$ to $N$. Find the minimum number of edges used in a path with length $K$ or print “-1” if the path doesn’t exist.
$1\le N \le 2\times 10^5, 1\le w_{i,j}\in \mathbb{N} \le 10^6, 1\le K \le 10^6$.
Problem analysis
Similar to the previous problem, we need to consider all possible paths. However, in this problem, instead of minimizing the distance of path, we need to find a specific value of path while minimizing the number of edges. Recall that centroid decomposition is a D&C algorithm. Let’s try to solve this problem using it. The divide part is easy, just collect answers from the subtrees (resulting from removing centroid). For the merge part, we need to consider paths that pass the current centroid. We can do a DFS to get the distance from centroid to its children. Then, do another DFS to get the answer. Look below for more details.
Problem solution
First, we do centroid decomposition on the tree. Let $u$ be the centroid. Then, we get the answer by the following algorithm:
Solve(u):
ans = inf
for v in child of u:
ans = min(ans, Solve(v))
do a DFS starting from u to calculate the distance and number of edges used
for nodes in component of u
do another DFS to calculate the answer, while using an array to keep track of
possible distances starting from u and the minimum edges needed
update ans from the previous DFS
return ans
The complexity is $(N\log N)$.
code
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N = (int)2e5 + 5;
const int M = (int)1e6 + 5;
const int inf = (int)1e9;
set<pair<int, int> > G[N];
int n, k, sz[N], exist[M], edgecnt[M], tt;
int dfs(int u, int p) {
sz[u] = 1;
for(auto it : G[u]) if(it.first != p) {
sz[u] += dfs(it.first, u);
}
return sz[u];
}
int centroid(int u, int p, int nn) {
for(auto it : G[u]) if(it.first != p) {
if(sz[it.first] > nn / 2) return centroid(it.first, u, nn);
}
return u;
}
int dfs2(int u, int p, int d, int cnt, int t, vector<pair<int, int> >& v) {
int want = k - d, ans = inf;
if(want >= 0 && exist[want] == t) {
ans = min(ans, cnt + edgecnt[want]);
}
if(d <= k) {
v.push_back({d, cnt});
for(auto it : G[u]) if(it.first != p) {
ans = min(ans, dfs2(it.first, u, d + it.second, cnt + 1, t, v));
}
}
return ans;
}
int Solve(int u, int p) {
int nn = dfs(u, p);
int c = centroid(u, p, nn);
int ans = inf;
int t = ++tt;
exist[0] = t; edgecnt[0] = 0;
for(auto it : G[c]) { // dfs one subtree at a time
vector<pair<int, int> > tmp;
ans = min(ans, dfs2(it.first, c, it.second, 1, t, tmp));
for(auto itt : tmp) {
if(exist[itt.first] != t || (exist[itt.first] == t && edgecnt[itt.first] > itt.second)) {
exist[itt.first] = t;
edgecnt[itt.first] = itt.second;
}
}
}
vector<pair<int, int> > tmp(G[c].begin(), G[c].end());
for(auto it : tmp) {
G[c].erase(it); G[it.first].erase({c, it.second});
ans = min(ans, Solve(it.first, c));
}
return ans;
}
void init() {
cin >> n >> k;
for(int i = 1 ; i < n ; ++i) {
int u, v, w; cin >> u >> v >> w;
G[u].insert({v, w});
G[v].insert({u, w});
}
}
void solve() {
tt = 0;
int ans = Solve(0, -1);
cout << (ans == inf ? -1 : ans) << '\n';
}
int main() {
ios_base::sync_with_stdio(0), cin.tie(0);
init();
solve();
}
Codechef - Prime Distance On Tree
Problem description
You’re given a tree with $N$ nodes. If we select 2 distinct nodes uniformly at random, what’s the probability that the distance between these 2 nodes is a prime number? Please calculate it.
Problem analysis
Obviously, we need to calculate number of pairs $(u, v)$ such that $dis(u, v)$ is a prime number. Again, we need to deal with all possible paths. Let’s try centroid decomposition. For a centroid $u$, we can first collect the answers from the subtree, then do convolution to calculate number of paths that pass $u$.
Problem solution
Do centroid decomposition on the tree. Then, for each centroid $u$, first solve it for children $v$, and maintain an array that record how many decendents are at each distance. Then, we can maintain the “decendent array” of $v$ be adding 1 to it. Finally, we use fft to calculate the number of paths that pass $u$ for each distance. We used the fact that $2\left(\sum_{i=1}^{n} \sum_{j=1}^{n} x_ix_j\right) = \left(\sum_{i=1}^{n}x_i\right)^2 - \sum_{i=1}^{n}x_i^2$. Details are given in the code.
The complexity will be $O(N\log N \times \log N)=O(N\log^2N)$ as the convolution part can be done in $O(N\log N)$ by fft.
code
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
typedef long double ld;
// ntt
// black magic: https://www.cnblogs.com/bibibi/p/9613151.html
inline ll mul(ll a, ll b, ll p) {
ll t = (a * b - (ll)((ld)a / p * b) * p);
return (t < 0 ? t + p : (t > p ? t - p : t));
}
template<ll P,ll root,int MAXK,int MAXN>
struct NTT{
static ll powi(ll a,ll b){
ll ret=1;
for(;b;b>>=1,a=mul(a, a, P)){
if(b&1) ret=mul(ret, a, P);
}
return ret;
}
static ll inv(ll a,ll b){
if(a==1) return 1;
return (((__int128)(a-inv(b%a,a))*b+1)/a)%b;
}
ll omega[MAXK+1],inv_omega[MAXK+1];
NTT(){
omega[MAXK]=powi(root,(P-1)>>MAXK);
for(int i=MAXK-1;i>=0;i--)
omega[i]=mul(omega[i+1], omega[i+1], P);
for(int i=0;i<=MAXK;i++)
inv_omega[i]=inv(omega[i],P);
}
void tran(int n,ll a[],bool inv_ntt=false){//n=2^i
for(int i=1,j=0;i<n;i++){
for(int k=n>>1;!((j^=k)&k);k>>=1);
if(i<j) swap(a[i],a[j]);
}
ll *G=(inv_ntt?inv_omega:omega);
for(int k=2,t=1;k<=n;k<<=1){
int k2=k>>1;ll dw=G[t++];
for(int j=0;j<n;j+=k){
ll w=1;
for(int i=j;i<j+k2;i++){
ll x=a[i],y=mul(a[i+k2], w, P);
a[i]=x+y; if(a[i]>=P) a[i]-=P;
a[i+k2]=x-y; if(a[i+k2]<0) a[i+k2]+=P;
w=mul(w, dw, P);
}
}
}
if(inv_ntt){
ll inv_n=inv(n,P);
for(int i=0;i<n;i++) a[i]=mul(a[i], inv_n, P);
}
}
};
const ll P=2061584302081,root=7;
const int MAXN=1048576,MAXK=20;//MAXN=2^i
struct PolyOp {
#define FOR(i, c) for (int i = 0; i < (c); ++i)
NTT<P, root, MAXK, MAXN> ntt;
ll aa[MAXN], bb[MAXN];
static int nxt2k(int x) {
int i = 1; for (; i < x; i <<= 1); return i;
}
void Mul(int n, ll a[], int m, ll b[], ll c[]) {
int N = nxt2k(n+m);
assert(N < MAXN);
copy(a, a+n, aa); fill(aa+n, aa+N, 0);
copy(b, b+m, bb); fill(bb+m, bb+N, 0);
ntt.tran(N, aa); ntt.tran(N, bb);
FOR(i, N) c[i] = mul(aa[i], bb[i], P);
ntt.tran(N, c, 1);
}
} polyop;
// ntt end
const int N = MAXN;
int n, sz[N];
ll ans[N], p1[N], p2[N], p3[N];
bitset<N> isp;
set<int> G[N];
map<int, int> cnt;
int dfs(int u, int p) {
sz[u] = 1;
for(auto v : G[u]) if(v != p) {
sz[u] += dfs(v, u);
}
return sz[u];
}
int centroid(int u, int p, int nn) {
for(auto v : G[u]) if(v != p) {
if(sz[v] > nn / 2) return centroid(v, u, nn);
}
return u;
}
void dfs2(int u, int p, int d) {
cnt[d]++;
for(auto v : G[u]) if(v != p) {
dfs2(v, u, d + 1);
}
}
void Solve(int u, int p) {
int nn = dfs(u, p), c = centroid(u, p, nn);
vector<int> tmp(G[c].begin(), G[c].end());
// calculate number of path that pass c
// we used the fact mentioned above
int len1 = nn;
fill(p1, p1 + len1, 0); p1[0] = 1;
fill(p3, p3 + len1, 0);
for(auto v : tmp) {
cnt.clear(); dfs2(v, c, 1);
int len2 = cnt.rbegin()->first + 1;
fill(p2, p2 + len2, 0);
for(auto pp : cnt) p2[pp.first] = pp.second, p1[pp.first] += pp.second;
polyop.Mul(len2, p2, len2, p2, p2);
for(int i = 0 ; i < len2 * 2 ; ++i) p3[i] += p2[i]; // \sum x_i^2, note that p2[0] = 0
}
polyop.Mul(len1, p1, len1, p1, p1); // (\sum x_i)^2, note that p1[0] = 1, because we need to calculate paths that start at c
for(int i = 0 ; i < len1 ; ++i) ans[i] += (p1[i] - p3[i]) / 2;
// calculate answer recursively
for(auto v : tmp) {
G[c].erase(v); G[v].erase(c);
Solve(v, c);
}
}
void init() {
cin >> n;
for(int i = 0 ; i < n - 1 ; ++i) {
int a, b; cin >> a >> b;
G[a].insert(b); G[b].insert(a);
}
}
void solve() {
Solve(1, 0);
isp.set(); isp[0] = isp[1] = 0;
for(int i = 2 ; i * i < N ; ++i) {
for(int j = i * i ; j < N ; j += i) isp[j] = 0;
}
ll ccnt = 0, sum = 0;
for(int i = 1 ; i <= n ; ++i) {
if(isp[i]) ccnt += ans[i];
sum += ans[i];
}
cout << fixed << setprecision(17) << (ld)ccnt / sum << '\n';
}
int main() {
ios_base::sync_with_stdio(0), cin.tie(0);
init();
solve();
}
More problems
- Codechef - Count It
- Here is a list of problmes solvable by centroid decomposition. Have fun!